2019-08-02 16:09:52
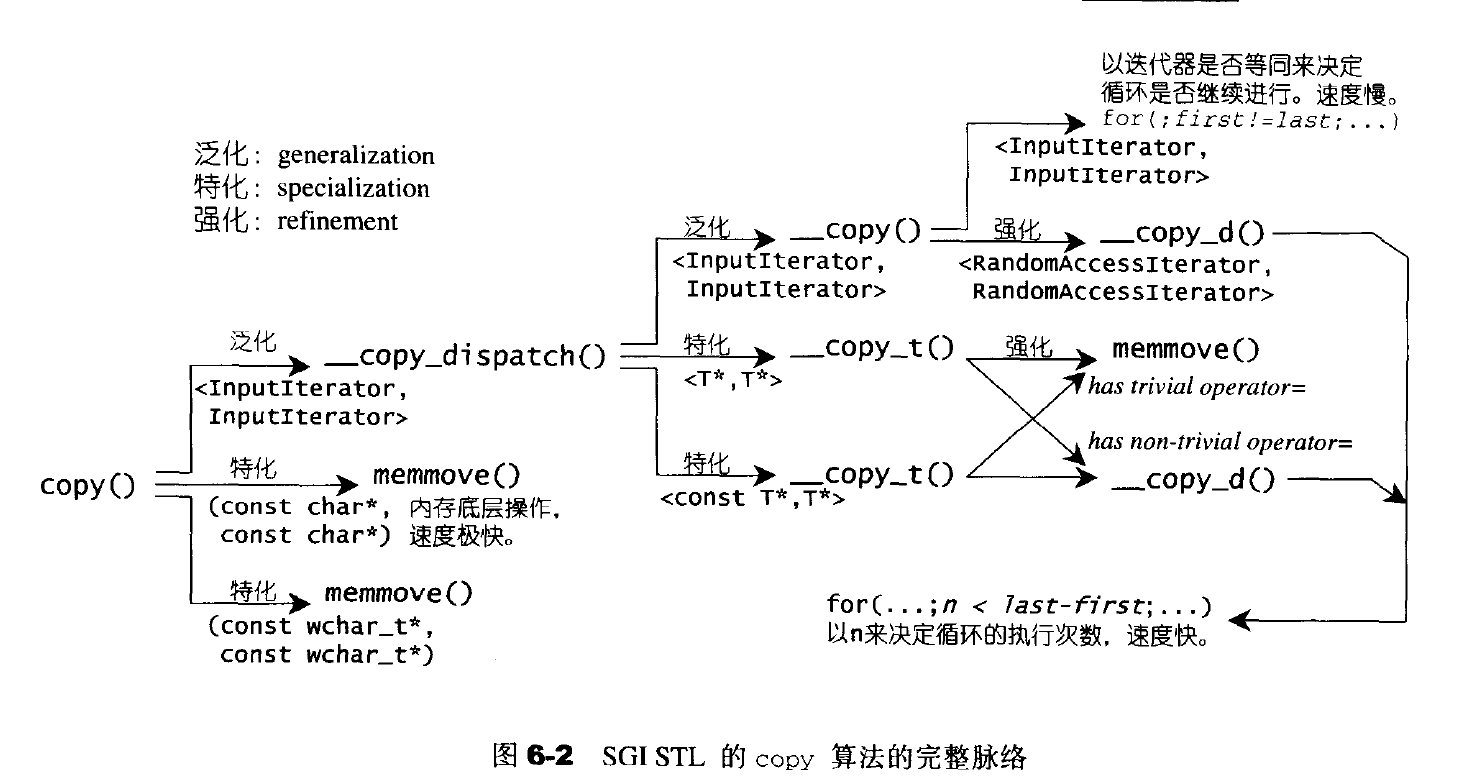
算法
算法总览和分类
STL算法总览




算法分类
- 质变算法:会改变操作对象之值;如copy、swap、replace、fill、remove、permutation、aprtition、random shuffling、sort等
- 非质变算法:不改变操作对象之值:find、search、count、for_each、equal、mismatch、max、min等
STL算法的一般形式
质变算法一半提供两个版本:in-place–就地改变操作对象;copy–将操作对象的内容复制一份副本(通常以_copy结尾),操作后返回。
6.3 数值算法
数值算法一般包含在表头
- accumulate 关键操作: init=init+i(第一版本)、init=binary_op(init,i*)(第二个版本)
- adjacent_difference:计算相邻元素的差额关键代码: i-(i-1);
- inner_product:能够计算一般内积,
result=result+(*i)**(first2+(i-first)) - partial_sum计算局部总和
- power:计算指数(C++中位运算的使用方法; STL源码分析之power算法;快速计算x的n次幂)
T power(T x,Integer n,Monoidoperation op)
{
if(n==0){
return identity_element(op);
}else{
//进行位运算直到为偶数,这里主要是为了过滤掉低位的0
while((n&1)==0){
n>>=1;
x=op(x,x);
}
//重新计算x,n变为偶数
T result=x;
n>>=1;
//
while(n!=0)
{
x=op(x,x);
//发现是奇数;将奇数去除,即乘一个x
if((n&1)!=0){
result=op(result,x);
}
//除以2
n>>=1;
}
return result;
}
}
/*
第一步判断n是否为0;
第一个while循环,尽可能的将底数变的更大,更好进行后续的计算,经过第一个while之后,n肯定是一个奇数了,再进入第二个循环,如果是1,则直接返回。
第二个while循环感觉就是求当前底数(x的偶数次平方,y)的奇数(m)次平方的过程,也就是求m的二进制各个位是否为1的过程,如果当前位M为1,则结果额外乘以y的2^M次方~
*/
在这里顺道测试了一下GCC的stl的性能,发现结果比较感人啊,迷之编译器优化。。。。
#include<bits/stdc++.h>
#include<cmath>
using namespace std;
//朴素算法
long pusu(int x,int n)
{
long num=1;
for(int i=0;i<n;i++)
{
num*=x;
}
return num;
}
//分治算法----快速幂
long fenzhi(int x,int n)
{
long num=1;
while(n)
{
if((n&1)!=0)
{
num*=x;
n--;
}
x*=x;
n/=2;
}
return num;
}
//stl算法
long stl_pow(int x,int n)
{
if (n == 0)
{
return 1;
}
else
{
while ((n & 1) == 0)
{
n >>= 1;
x *= x;
}
}
long result = x;
n >>= 1;
while (n != 0)
{
x *= x;
if ((n & 1) != 0)
result *= x;
n >>= 1;
}
return result;
}
int main()
{
int x=3,n=5,k=2;
//cin>>x>>n;
for(int i=0;i<k;++i){
++x;
for(int j=0;j<k;++j){
++n;
long result;
clock_t start_time=clock();
long temp1=pusu(x,n);
cout<<"朴素算法结果:"<<temp1<<endl;
clock_t end_time=clock();
printf("Running time is: %lfms\n",static_cast<double>(end_time-start_time)/CLOCKS_PER_SEC*1000);
clock_t start_time1=clock();
long temp2=fenzhi(x,n);
cout<<"分治算法结果:"<<temp2<<endl;
clock_t end_time1=clock();
printf("Running time is: %lfms\n",static_cast<double>(end_time1-start_time1)/CLOCKS_PER_SEC*1000);
clock_t start_time2=clock();
cout<<"STL_power:"<<stl_pow(x,n)<<endl;
clock_t end_time2=clock();
printf("Running time is: %lfms\n",static_cast<double>(end_time2-start_time2)/CLOCKS_PER_SEC*1000);
clock_t start_time3=clock();
cout<<"STL结果:"<<std::pow(x,n)<<endl;
clock_t end_time3=clock();
printf("Running time is: %lfms\n",static_cast<double>(end_time3-start_time3)/CLOCKS_PER_SEC*1000);
printf("x %d,n %d \n",x,n);
printf("--------------------\n");
}
}
return 0;
}
/* 结果
朴素算法结果:4096
Running time is: 0.097000ms
分治算法结果:4096
Running time is: 0.006000ms
STL_power:4096
Running time is: 0.009000ms
STL结果:4096
Running time is: 0.025000ms
x 4,n 6
--------------------
朴素算法结果:16384
Running time is: 0.006000ms
分治算法结果:16384
Running time is: 0.005000ms
STL_power:16384
Running time is: 0.007000ms
STL结果:16384
Running time is: 0.009000ms
x 4,n 7
--------------------
朴素算法结果:390625
Running time is: 0.005000ms
分治算法结果:390625
Running time is: 0.007000ms
STL_power:390625
Running time is: 0.007000ms
STL结果:390625
Running time is: 0.009000ms
x 5,n 8
--------------------
朴素算法结果:1953125
Running time is: 0.006000ms
分治算法结果:1953125
Running time is: 0.007000ms
STL_power:1953125
Running time is: 0.006000ms
STL结果:1.95312e+06
Running time is: 0.009000ms
x 5,n 9
--------------------
*/
6.4 基本算法
基本常用算法定义在
基本函数有: equal,fill,fill_n,iter_swap,lexicographical_compare,max,min,mismatch,swap;这些在之前的c++primer阅读笔记中有介绍,不再过多赘述。
lexicographical_compare:字典排列方式对两个序列,进行比较
- 如果第一序列的元素较小,返回true,否则返回false
- 如果达到last1而尚未达到last2,返回true
- 如果达到last2而尚未达到last1,返回false
- 同时达到,返回false
当复制位置的起点在复制区间内时,将会发生错误。为了防止上述错误的发生,一般都会先把目标区段使用memmove()复制下来,再进行操作。
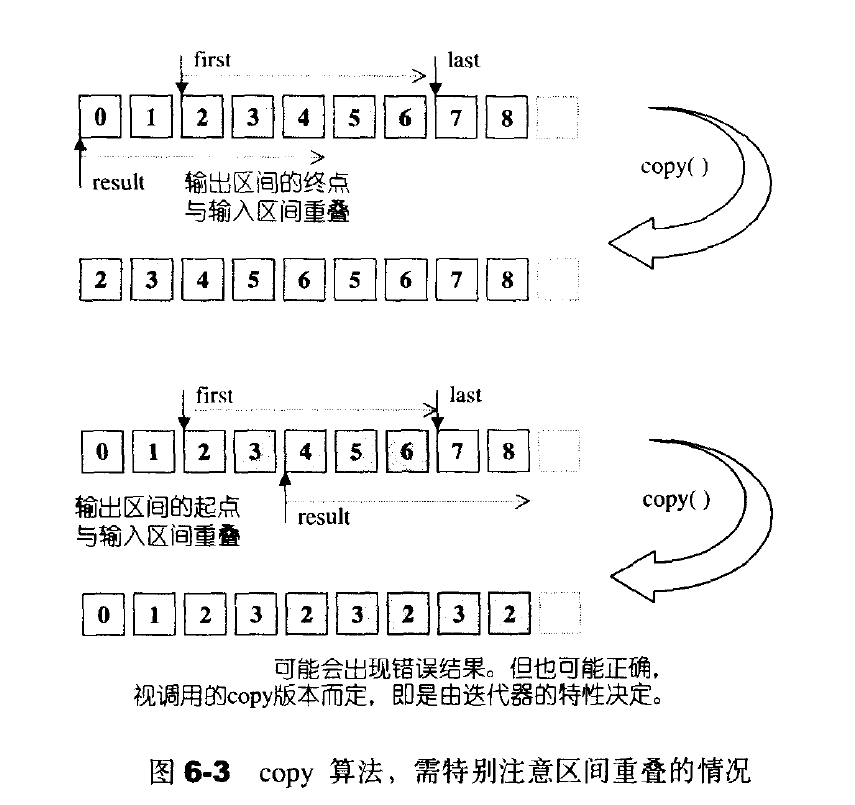
copy改变的是[result,result+(last-first))中的迭代器所指对象,而并非更改迭代器本身。它会为输出区间的元素赋予新值,而不是产生新的元素。它不能改变输出区间的迭代器个数。因此不能将元素插入空容器中。
copy_backward 反向拷贝
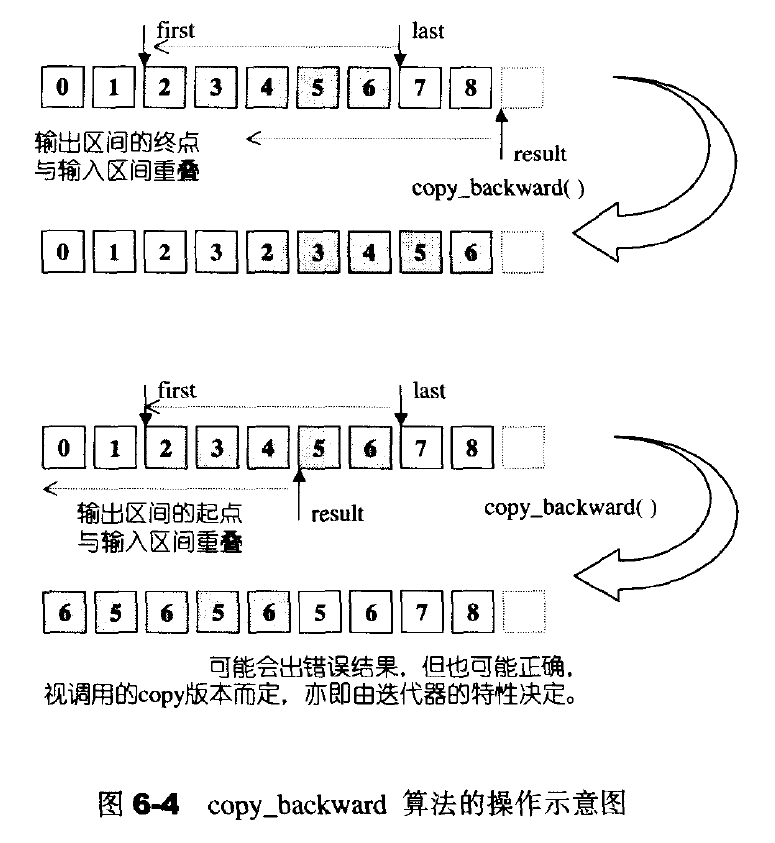
6.5 set 相关算法
STL提供了四种set(集合)相关的算法,分别是并集(union),交集(intersection),差集(difference)、对称集(symmetic difference)
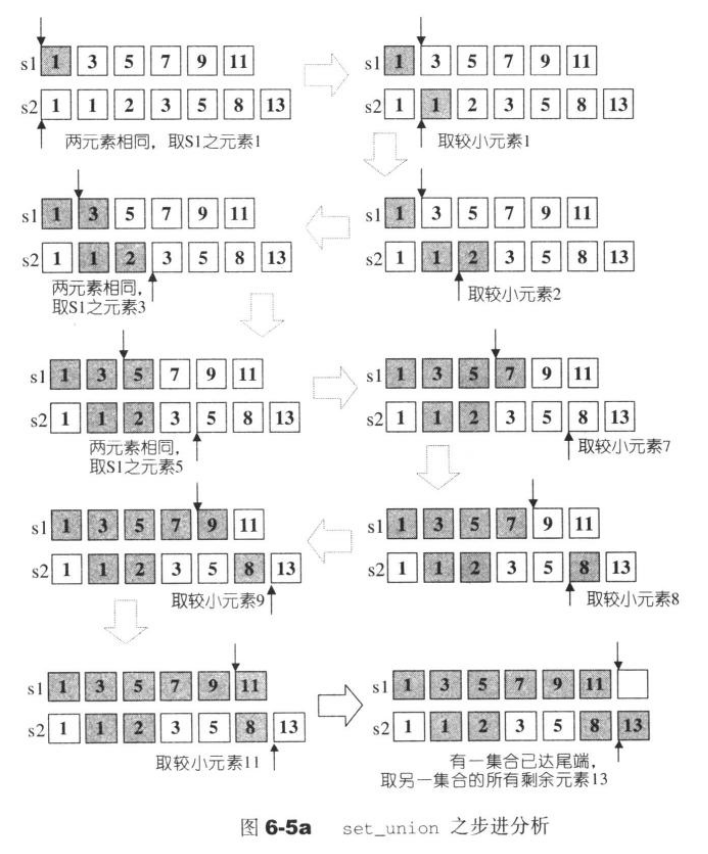
set_union:求并集–set_union(first1,last1,first2,last2,ostream_iterator
比较的关键代码:
template <class InputIterator1,class InputIterator2,class OutputIterator>
OutputIterator set_union(InputIterator1 first1,InputIterator1 last1,
InputIterator2 first2,InputIterator2 last2)
{
while(first1!=last1&&first2!=last2) {
//在两个区间之内分别移动迭代器,首先将元素较小者(假设为A区)记录于目标区域;然后移动A区迭代器使之前进;同时另一个迭代器不懂,然后进行新一次的比较大小、记录值、迭代器、迭代器移动,直到两区中有一个区达到尾端。如果元素相等,取S1者记录于目标区,并同时移动两个迭代器
if(*first1<*first2){
*result=*first1;
++first1;
}else if(*first2<*first1){
*result=*first2;
++first2;
//*first2==*first1
}else{
*result=*first1;
++first1;
++first2;
}
++result;
}
}
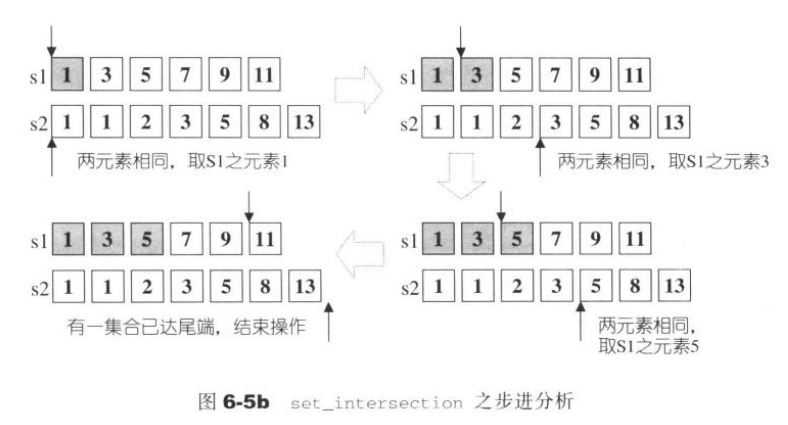
6.5.2 set_intersection构造交集
基本上就是上面的条件判断反过来了,当相等时迭代器才增加。
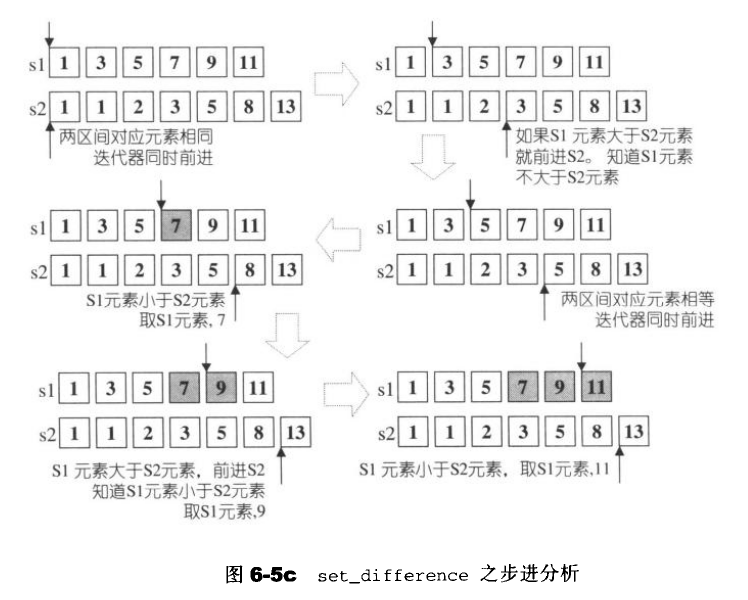
6.5.3 set_difference
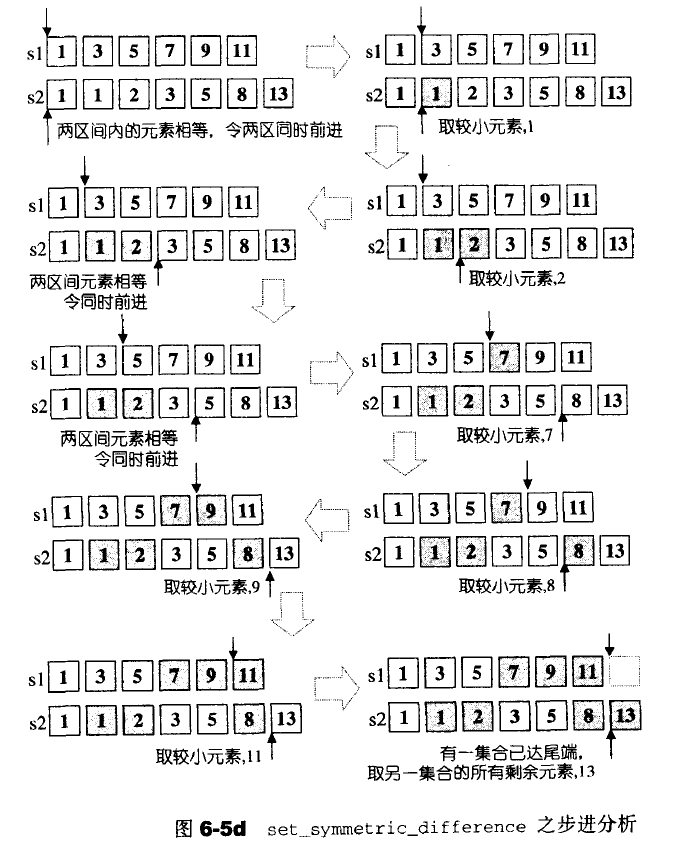
6.5.4 set_symmetric_difference 构造对称差集
6.7 其它算法
find_end:查找最后一次出现的点
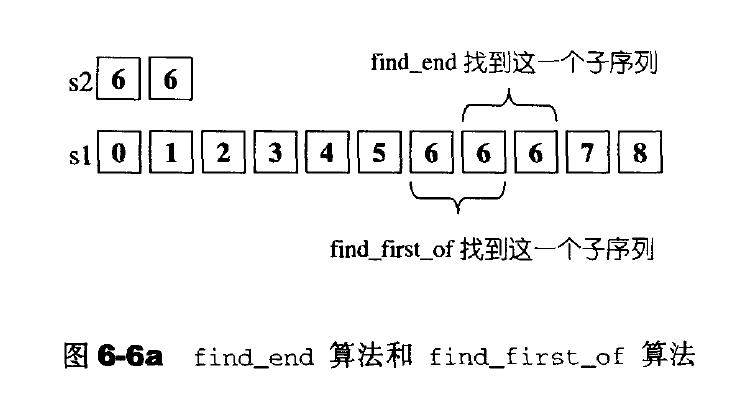
includes(应用于有序区间)
判断序列s2是否“涵盖于”序列s1。
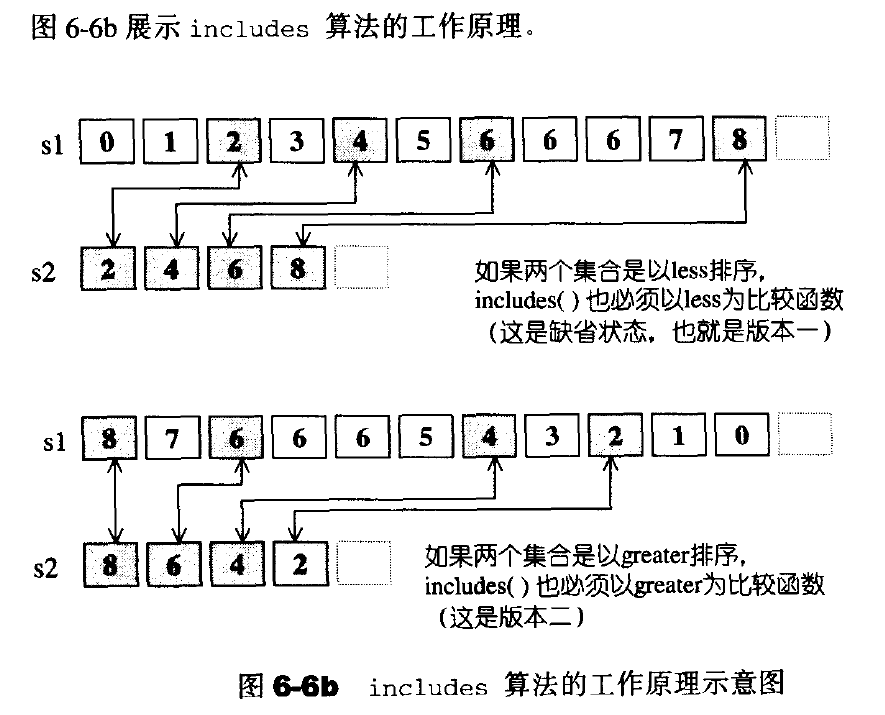
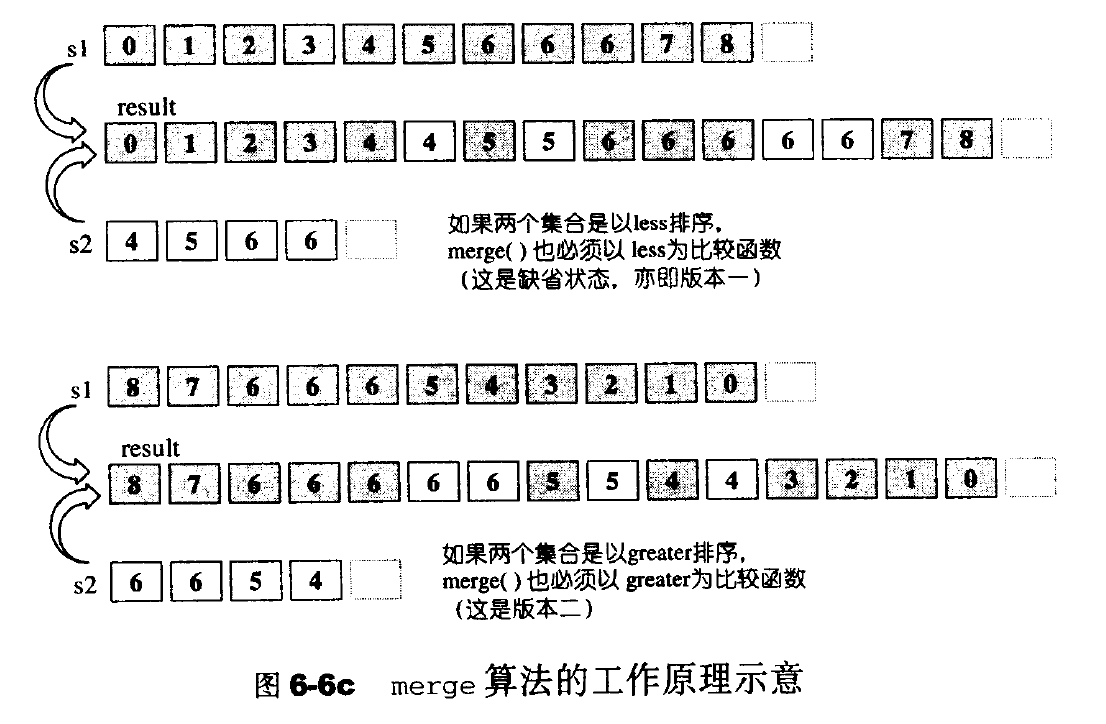
merge 将两个经过排序的集合S1和S2,合并起来置于另一段空间。所得结果也是一个有序(sorted)序列。
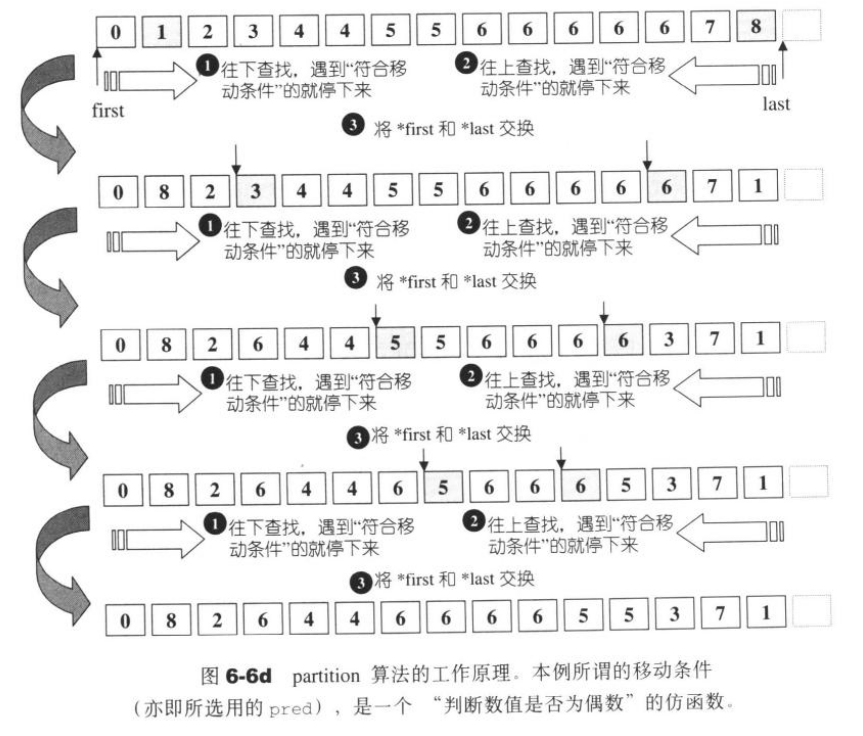
paritition 将区间中的元素重新排列,通过条件进行筛选。这个算法并不保证保留元素的原始相对位置,如果需要保留原始相对位置,应该使用stable_partition
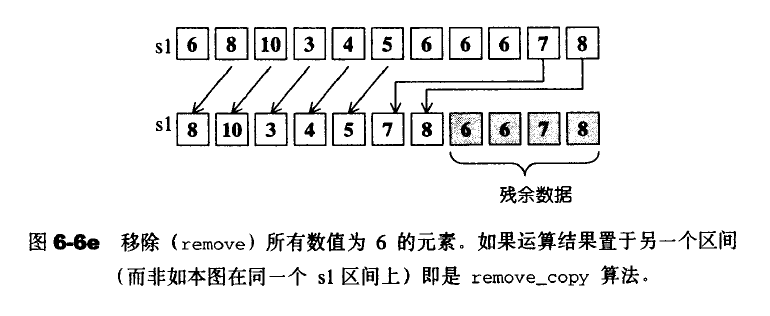
remove
remove并不真正的删除这个元素,而是将每一个不与value相等的匀速轮番赋值给first之后的空间。返回值表示重新整理之后的最后元素的下一个位置。例如{0,1,0,2,0,3,0,4};执行remove(0);最终结果为{1,2,3,4,0,3,0,4};返回的Forwarallterator指向第五个位置。如果要进行删除需要使用erase()来将迭代器后面的数据进行删除。注意array不适合使用remove()和remove_if();因为它无法缩小尺寸,导致残余数据永远存在。应该使用remove_copy()和remove_copy_if();
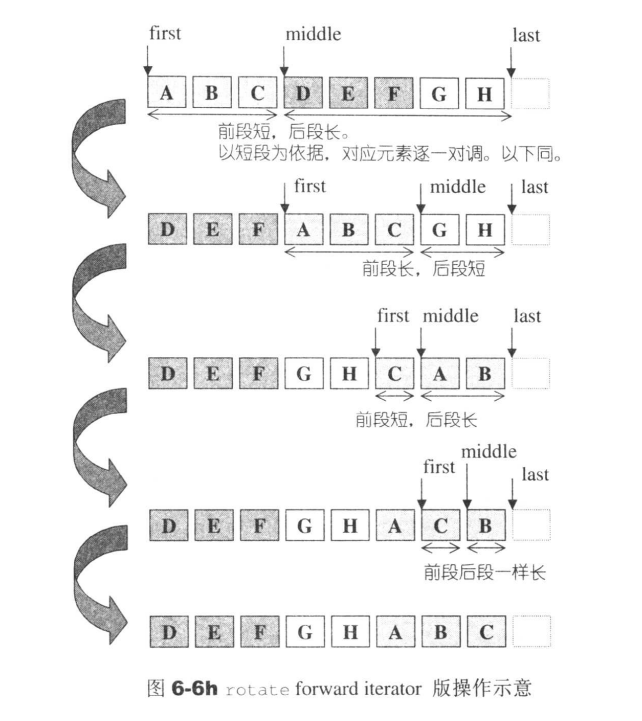
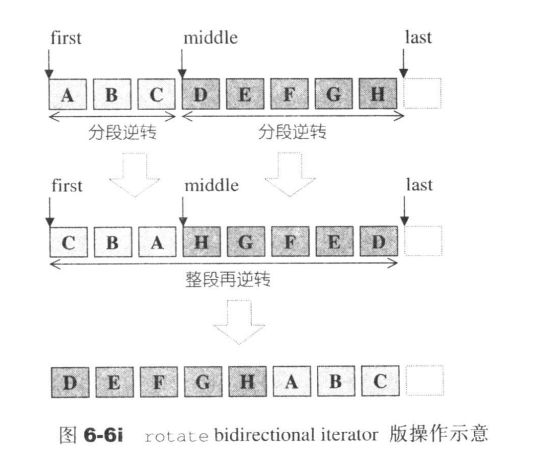
rotate
rotate可以实现非对称的位置交换。
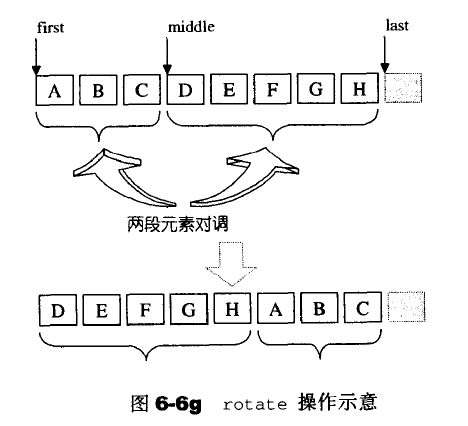 关键代码:
关键代码:
template <class ForwardIterator,class Distance>
void __rotate(ForwardIterator first,ForwardIterator middle,ForwardIterator last,Distance*,forward_iterator_tag)
{
for(ForwardIterator i=middle;;)
{
//前段后段的元素一一交换
iter_swap(first,i);
//双双前景
++first;
++i;
//判断那个先行结束
//前段先行结束
if(first==middle)
{
//后段同时结束,整个就结束了
if(i==last) return;
//调整位置,对新的前后段再做交换
middle=i;
//后段先结束
}else if(i==last){
//调整,准备对新的前后段再做交换
i=middle;
}
}
}
unique移除重复的元素
注意:unique只移除相邻的重复元素,如果你想移除所有重复元素,必须先行排序。 所有保留下来的元素,其原始值相对次序不变
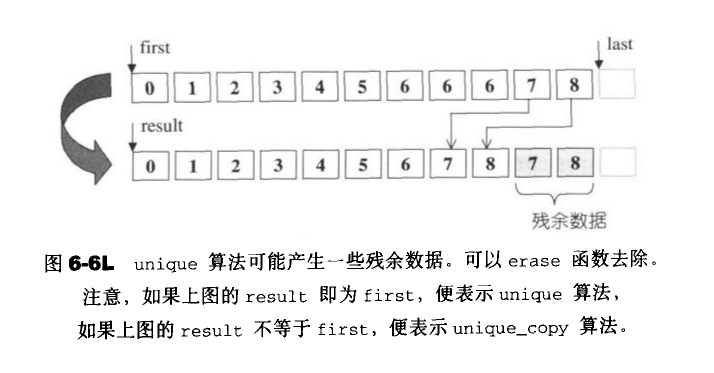
lower_bound/upper_bound(应用于有序区间)
这个是二分查找的一种版本,试图在已经排序的[first,last)中寻找匀速value。返回满嘴条件的第一个元素。upper_bound是返回最后一个值
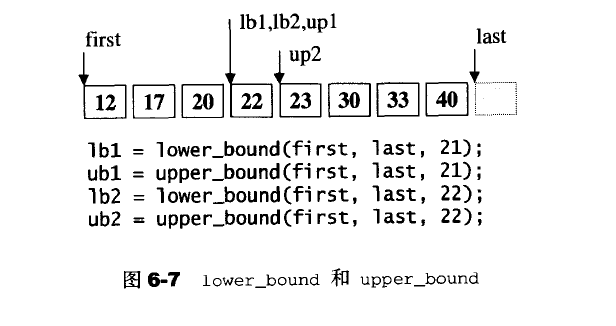
next_permutation
取得[first,last)所标示的下一个排列组合,有就返回true,否则返回false。
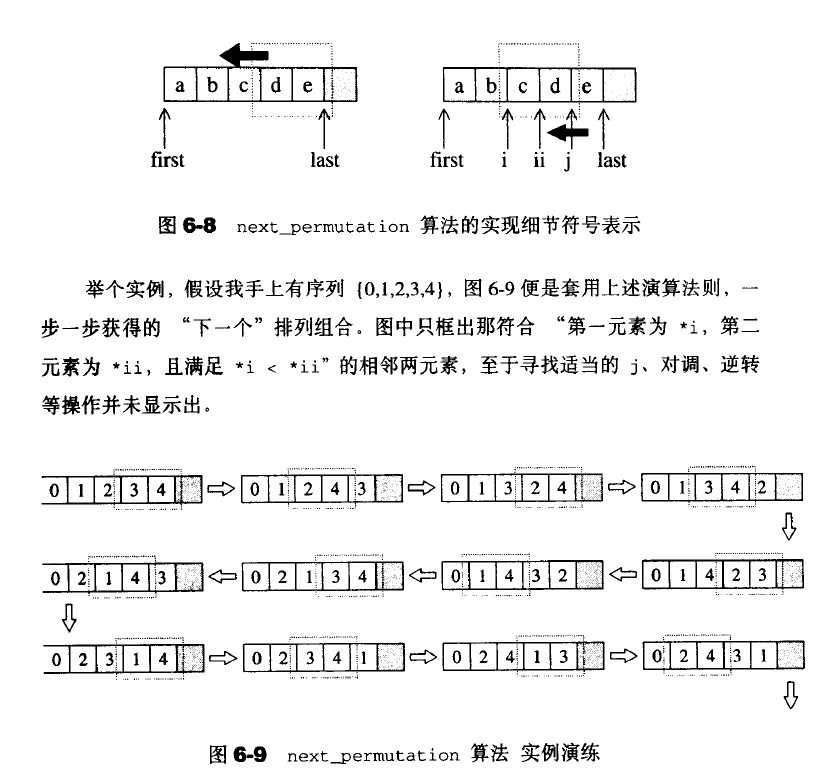
next_permutation 与上面基本相同
random_shuffle
将元素次序随机重排。
6.7.9 sort
这个算法接受两个RandomAccesslterators(随机存取迭代器),然后将区间内的所有元素以渐增方式由小到大重新排列。并且存在允许用户使用仿函数来进行排序。STL的所有关系型容器都拥有自动排序功能(底层采用RB-tree);所以不需要用到这个sort算法。序列式容器中的stack,queue,priority-queue都有特定的出入口,不允许用户对元素排序。vector和dequeue适合使用sort算法。list的迭代器鼠疫Bldirectionaltterators不适合使用sort算法。
STL的sort算法数据量大的时候采用Quick Sort(现在已经开始使用IntroSort 最坏算法复杂度为O(NlogN)) ;数据量小的时候使用Insertion Sort。主要是因为插入排序在数据量很小的时候有不错的效果。并且没有额外的开销和负荷。
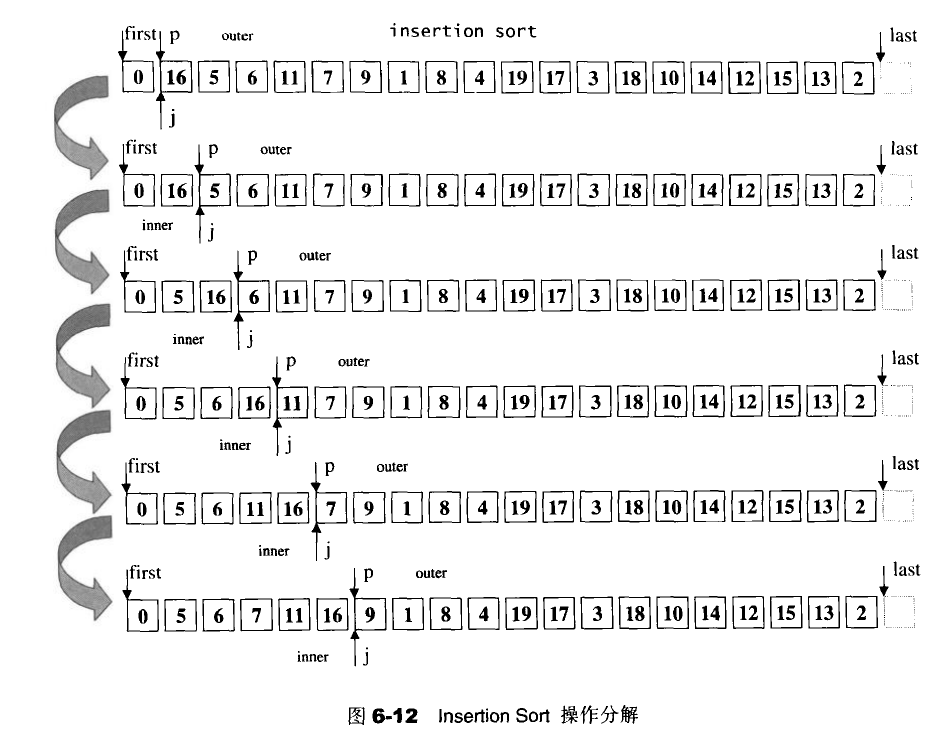
注意:这里是采用交换的方式进行的排序,不是链表的指直接插入。
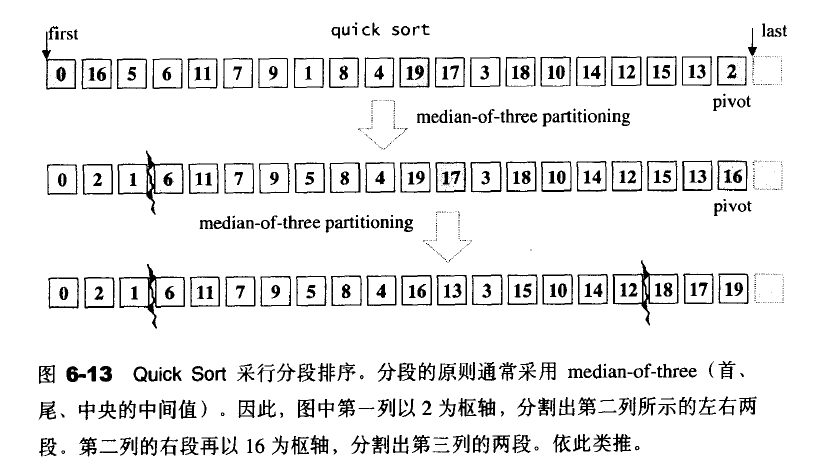
快速排序的一般流程
- 如果S的元素个数为0或者1,结束
- 取S中的任何一个元素,当做轴(pivot)v。
- 将s分割为L,R;两段,使得L内的每一个元素都小于或者等于v,R内的每一个元素都大于或等于v。
- 对L,R递归执行Quick Sort
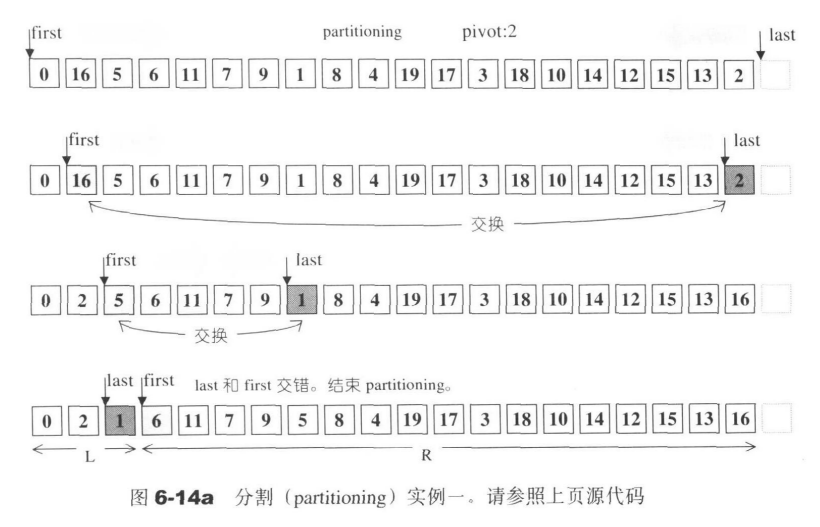
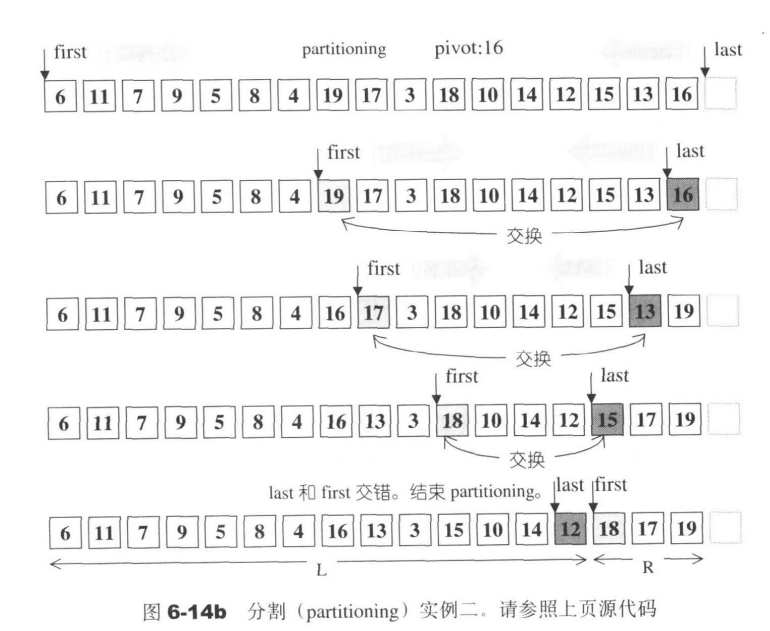
下面是快速排序的具体代码
template <class RandomAccessIterator>
inline void sort(RandomAccessIterator first,
RandomAccessIterator last
)
{
if(first!=last){
__introsort_loop(first,last,value_type(first),__lg(last-first)*2);
__final_insertion_sort(first,last);
}
}
//__lg()用来控制分割恶化的情况
//找出2^k<=n的最大值K,例如n=7,k=2,n=20,k=4;
template <class Size>
inline Size __lg(Size n)
{
Size k;
for(k=0;n>1;n>>=1) ++k;
return k;
}
//返回a,b,c之间的居中者
template <class T>
inline const T& __median(const T& a,const T& b,const T& c)
{
if(a<b){
if(b<c){
return b;
}else if(a<c){
return c;
}else{
return a;
}
}else if(a<c){
return a;
}else if(b<c){
return c;
}else {
return b;
}
}
//数组分割返回分割后的右段的第一个位置
template <class RandomAccessIterator,class T>
RandomAccessIterator __unguarded_partition(
RandomAccessIterator first,
RandomAccessIterator last,
T pivot)
{
while(true){
//找到>=pivot的元素就停下来
while(*first<pivot){++ first;}
//调整指针位置
--last;
//找到<=pivot的元素就停下来。
while(pivot<*last) --last;
//注意一下只适用于 random iterator
//交错,结束循环
if(!(first<last)) return first;
//大小值交换
iter_swap(first,last);
//调整
++first;
}
}
//当匀速个数为40时,__introsoft_loop()的最后一个参数将是5*2,意思是最多允许分割10层。IntroSort算法如下:
template <class RandomAccessIterator,class T,class Size>
void __introsort_loop(RandomAccessIterator first,
RandomAccessIterator last,
T*,
Size depth_limit)
{
//__stl_threshold是一个全局常数,稍早定义为const int 16
while(last-first>__stl_threshold) {
if(depth_limit==0){
//分割恶化,改用heapsort
partial_sort(first,last,last);
return;
}
--depth_limit;
//选择一个够好的轴枢并决定分割点,并赋值给cut
RandomAccessIterator cut=__unguarded_partition(first,last,T(__median(*first,*(first+(last-first)/2),*(last-1))));
//根据cut对右半段递归进行sort
__introsort_loop(cut,last,value_type(first),depth_limit);
last=cut;
//这里是回到while循环,准备对左半段递归进行sort
}
}
6.7.10 equal_range(应用于有序区间)
是二分查找法的一个版本。试图在已排序的[first,last)中寻找value。它返回一对迭代器i和j,i是在不破坏次序的前提下,value可以插入的第一个位置,j则是最后一个。因此i-j内都是value。
6.7.11 inplace_merge(应用于有序区间)
将两个已经有序的序列重新结合成为一个新的有序序列。注意,这个算法会使用额外的内存空间(暂时缓冲区)。
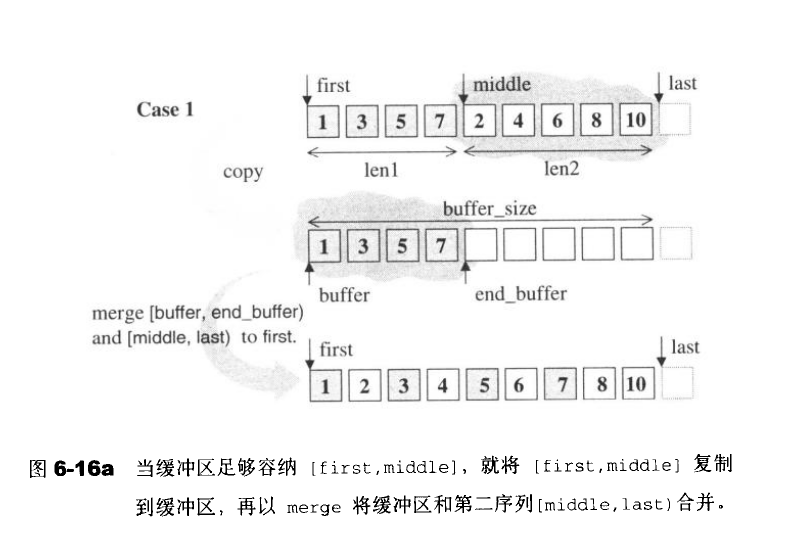
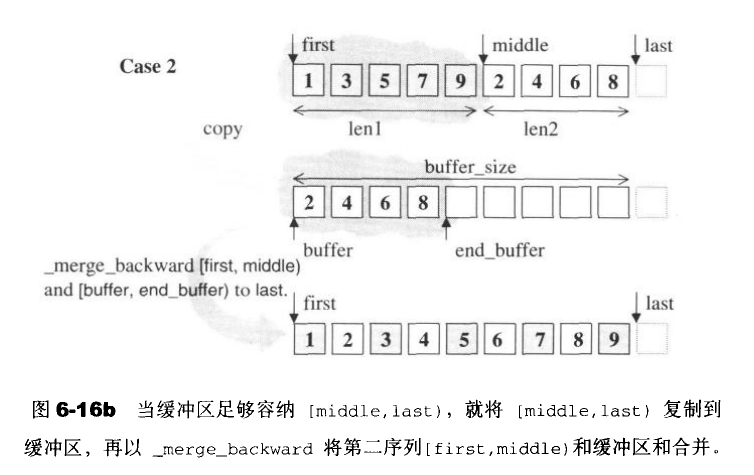
6.7.12 nth_element
重新排列,使得迭代器nth所指的元素,与整个迭代队列完整排序之后,同一位置的元素同值。同时保证[nth,last)内没有任何一个元素不大于[first,nth);但对于[first,nth)和[nth,last)两个子区间内的元素次序则无任何保证。
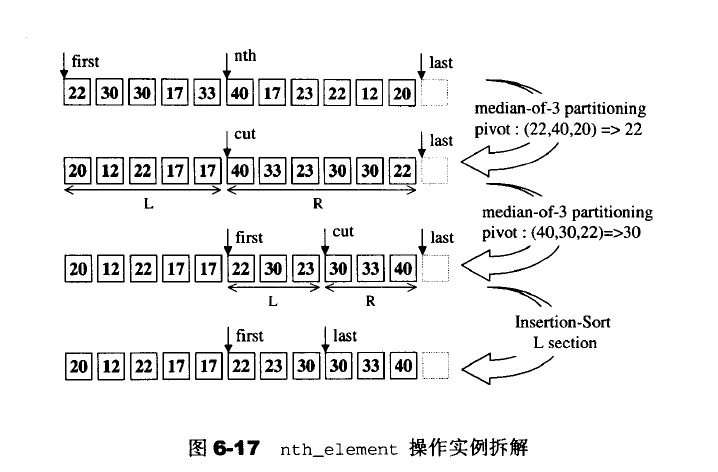
6.7.13 merge sort
利用分治思想,以各个击破的方式来对区间进行排序:
- 将区间对半分开,左右两段各自排序。
- 使用inplace_merge重新组合为一个完整的有序序列
- 递归对半操作,直到每一小段的长度为0或者1.
merge sort的算法复杂度是是O(NlongN)但是因为使用了额外的资源,因此性能反而不如Quick Sort
template <class BidirectorIter>
void mergesort(BidirectorIter first,BidirectorIter last)
{
typename iterator_traits<BidirectorIter>::difference_type n=distance(first,last);
if(n==0||n==1)
{
return;
}else{
BidirectorIter mid=first+n/2;
mergesort(first,mid);
mergesort(mid,last);
inplace_merge(first,mid,last);
}
}