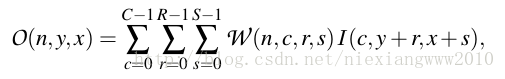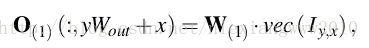所有卷积方式和算法的集合
参考链接:
2019-10-12 12:59:34
几种矩阵存储模式:
LibSVM格式(官网链接)
一种通用的训练数据格式,主要用在xboost等机器学习和深度学习中
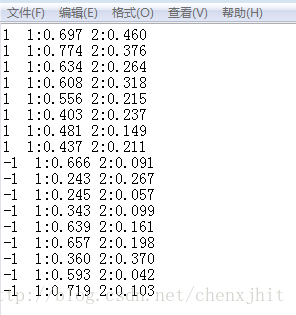
[label] [index1]:[value1] [index2]:[value2] …
[label] [index1]:[value1] [index2]:[value2] …
label 目标值,就是说class(属于哪一类),就是你要分类的种类,通常是一些整数。
index 是有顺序的索引,通常是连续的整数。就是指特征编号,必须按照升序排列
value 就是特征值,用来train的数据,通常是一堆实数组成。 具体实例入下面所示:
COO:Coordinate
将矩阵中不为0的数的行号、列号和数值对应存储下来:
优缺点
- 优点:比较容易转换成其他的稀疏矩阵存储格式(CSR等),写程序将libsvm格式的数据转换成COO比较容易,应该是充当libsvm与其他稀疏矩阵存储格式转换的媒介。
- COO缺点:不能进行矩阵运算。
下面是一个读取libSVM数据格式并转换成COO的代码
# 读取libsvm格式数据成稀疏矩阵形式
# 0 5:1 9:1 140858:1 445908:1 446177:1 446293:1 449140:1 490778:1 491626:1 491634:1 491641:1 491645:1 491648:1 491668:1 491700:1 491708:1
def read_data(file_name):
X = []
D = []
y = []
with open(file_name) as fin:
for line in fin:
fields = line.strip().split()
y_i = int(fields[0])
X_i = [int(x.split(':')[0]) for x in fields[1:]]
D_i = [int(x.split(':')[1]) for x in fields[1:]]
y.append(y_i)
X.append(X_i)
D.append(D_i)
y = np.reshape(np.array(y), [-1])
X = libsvm_2_coo(zip(X, D), (len(X), INPUT_DIM)).tocsr()
return X, y
# 将libSVM转换成COO代码
def libsvm_2_coo(libsvm_data, shape):
coo_rows = []
coo_cols = []
coo_data = []
n = 0
for x, d in libsvm_data:
coo_rows.extend([n] * len(x))
coo_cols.extend(x)
coo_data.extend(d)
n += 1
coo_rows = np.array(coo_rows)
coo_cols = np.array(coo_cols)
coo_data = np.array(coo_data)
return coo_matrix((coo_data, (coo_rows, coo_cols)), shape=shape)
CSR:按行压缩存储
CSR是比较标准的一种,也需要三类数据来表达:
- 数值,
- 列号,
- 以及行偏移。
CSR不是三元组,而是整体的编码方式。数值和列号与COO一致,表示一个元素以及其列号,行偏移表示某一行的第一个元素在values里面的起始偏移位置。row offsetS的数值个数是 #row+1,
如下图中,0,2,4,7分别表示第一行、第二行、第三行、第四行的第一个非零元素在values的位置。第一行元素1是0偏移,第二行元素2是2偏移,第三行元素5是4偏移,第4行元素6是7偏移。在行偏移的最后补上矩阵总的元素个数,本例中是9。其中column indices记录的是对应的value所在列的index。比如1在0列,7在1列;4在三列。
优缺点
本质上还是对于非零元素的去除,并没有去除其中的重复元素。
- 优点:
- 高效的CSR + CSR
- CSR*CSR算术运算
- 高效的行切片操作
- 高效的矩阵内积内积操作
- CSR格式在存储稀疏矩阵时非零元素平均使用的字节数(Bytes per Nonzero Entry)最为稳定(float类型约为8.5,double类型约为12.5)
- CSR格式常用于读入数据后进行稀疏矩阵计算。
- 缺点:
- 列切片操作慢(相比CSC)
- 稀疏结构的变化代价高(相比LIL或者DOK)
假设B为大矩阵,S为小矩阵。 当CSR格式时,S×B速度较快,与B×S相比节约了一半时间。 当CSC格式时,B×S速度较快,与S×B相比节约一半时间。
CSC:按列压缩存储
CSC是和CSR相对应的一种方式,即按列压缩的意思。 以上图中矩阵为例: Values:[1 5 7 2 6 8 3 9 4] Row Indices:[0 2 0 1 3 1 2 2 3] Column Offsets:[0 2 5 7 9]
直接稀疏卷积(Direct Sparse Convolution)
参考链接:
- 论文原文:地址
- [论文总结]:faster cnns with direct sparse convolutions and guided pruning 直接稀疏卷积和引导剪枝
- ICLR2017 paper: FASTER CNNS WITH DIRECT SPARSE CONVOLUTIONS AND GUIDED PRUNING 笔记
- 稀疏卷积神经网络
- 项目地址:https://github.com/IntelLabs/SkimCaffe
- 关键代码地址https://github.com/IntelLabs/SkimCaffe/blob/intel_scnn/include/caffe/util/sconv.hpp
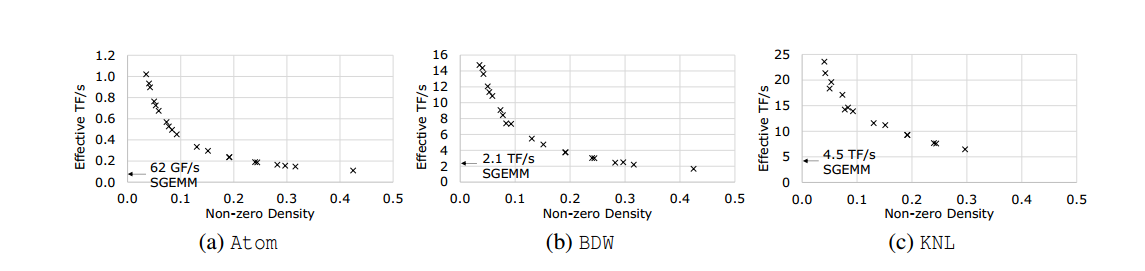
下面是稀疏卷积分解的主要流程对比图:

算法介绍
稀疏卷积可以看作抽象的sparse-matrix-dense-matrix multiplication
假设有N个filters,每个的size为R × S. 输入为C×H×W,于是这层的参数为一个N × C × R × S的张量,input是C × H(in)× W(in)的张量,output为C × H(out)× W(out)的张量,如下:两个三维张量的点积
这个操作可以被看成首先根据channnels向量化4维的blob,然后再向量化kernel最后再按照二维点乘的方式计算。当W稀疏时,就变成了一个sparse-vector-dense-vector点乘。
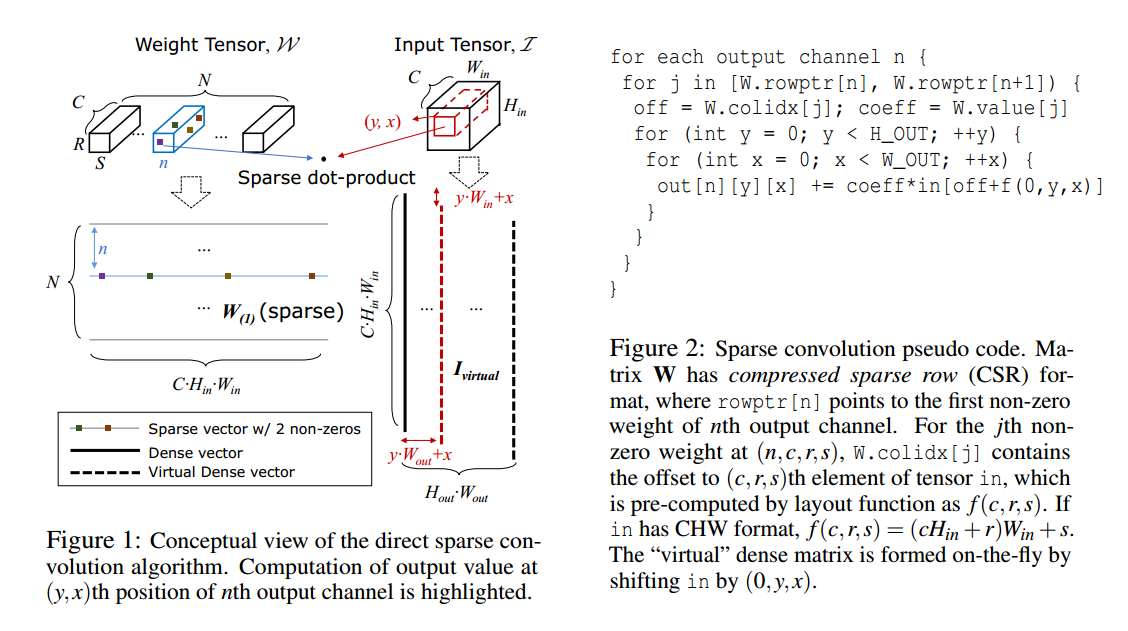
- 先将权重矩阵W按第一维展平,得稀疏矩阵W(1),并且row vectors和vec(I)的维数匹配。
- O(n,y,x)是W(1)的第n行和vec(I)之间的点积。
- 于是每个点(x,y)处的卷积结果可以计算多个sparse-matrix-dense-vector multiplication 来得到。
- I y,x代表张量I根据(y,x)变化得到的向量化结果。
- 于是就可以定义一种虚拟的dense matrix,每个column都是快速且独立生成的。
下面是实际的关键代码
void caffe_cpu_sconv_default(
// 输入的特征图
const float *input_padded,//特征图数据
int in_channels,//输入通道数量
int height,//输入高度
int width,//输入宽度
int pad_h, int pad_w,//宽高扩展
int stride_h, int stride_w,//高宽步长
int dilation_h, int dilation_w,//宽高上的缩放尺寸,也就是线性差值尺寸
// weights,权重数据,注意权重数据是以CSR数据格式保存的。
const int *rowptr,//行数据
const int *colidx, //列index索引
const float *values,//最终值
int kernel_h, int kernel_w,//卷积核的高宽
const float *bias,//基础偏移
// output features
float *output,//输出数据
int out_channels//输出通道数目
)
{
//计算输出高宽
const int output_h = (height + 2 * pad_h -
(dilation_h * (kernel_h - 1) + 1)) / stride_h + 1;
const int output_w = (width + 2 * pad_w -
(dilation_w * (kernel_w - 1) + 1)) / stride_w + 1;
//设置循环卷积batch
conv_cycles_of_this_batch[omp_get_thread_num()*16] = __rdtsc();
//如果缩放不为1
if (dilation_h != 1 || dilation_w != 1) {
for (int output_row = 0; output_row < output_h; ++output_row) {
for (int output_col = 0; output_col < output_w; ++output_col) {
for (int oc = 0; oc < out_channels; ++oc) {
float sum = bias[oc];
for (int j = rowptr[oc]; j < rowptr[oc + 1]; ++j) {
int off = colidx[j];
int kernel_col = off%(width + pad_w);
int kernel_row = (off/(width + pad_w))%(height + pad_h);
int in_channel = off/((width + pad_w)*(height + pad_h));
int input_row = kernel_row * dilation_h + output_row * stride_h;
int input_col = kernel_col * dilation_w + output_col * stride_w;
sum += values[j]*input_padded[(in_channel * (height + pad_h) + input_row) * (width + pad_w) + input_col];
}
output[(oc * output_h + output_row) * output_w + output_col] = FUSE_RELU ? std::max(0.f, sum) : sum;
}
}
}
}
else {//卷积缩放为1,没有缩放
for (int output_row = 0; output_row < output_h; ++output_row) {//输出行遍历
for (int output_col = 0; output_col < output_w; ++output_col) {//输出列遍历
//获取当前指针指向数据=起点指针+输出行*行步长*(输入宽度+扩展宽度)+输出列*列步长;这里相当于是使用输出点的坐标,反向计算输入点应该的坐标,注意这里没有加通道
const float *in = input_padded + output_row * stride_h * (width + pad_w) + output_col * stride_w;
//按照输出通道数目进行遍历,输出通道数目=输入通道数目
for (int oc = 0; oc < out_channels; ++oc) {
//获取每个的基础地址
float sum = bias[oc];
//按照行对每个权重进行
for (int j = rowptr[oc]; j < rowptr[oc + 1]; ++j) {//j是当前通道数目到下一个通道数目之间
//检查数据是否越界
assert(in + colidx[j] >= input_padded && in + colidx[j] < input_padded + in_channels*(width + pad_w)*(height + pad_h) + pad_h*(width + 2*pad_w));
//和=权重值*对应数据;注意这里是通道数目的乘法,对应的是(c,x,y)中c的变化
sum += values[j]*in[colidx[j]];
}
//最后计算输出的index
output[(oc*output_h + output_row)*output_w + output_col] = FUSE_RELU ? std::max(0.f, sum) : sum;
}
}
}
}
conv_cycles_of_this_batch[omp_get_thread_num()*16] = __rdtsc() - conv_cycles_of_this_batch[omp_get_thread_num()*16];
}
算法重述
- 将输入(C,W,H)数据压缩成为一个一维数组,其中(w,h,c),其中每个起点之后是连续的c个数据,代表不同通道上的数据
- 将权重数据按照CSR方式进行存储,最后一个维度也是c。
- 按照通道进行计算和相加
从本质上来说稀疏卷积,只是对于已经压缩存储的权重数据的优化,相对直接卷积来说,以w*h为主要遍历对象,直接进行c上的多个数据计算和相加,主要避免了数据的多次访问,提高了计算效率。相对于原来的二维直接卷积,先计算每个卷积矩阵点乘,再将c个矩阵相加减少了m*n的时间复杂度,提高了利用率。预计提高速度1.5~3。矩阵越稀疏,效果越明显