面试中的海量数据处理问题总结:

参考链接:

0. 基础知识

所谓海量数据处理，无非就是基于海量数据上的存储、处理、操作。何谓海量，就是数据量太大，所以导致要么是无法在较短时间内迅速解决，要么是数据太大，导致无法一次性装入内存。

针对时间，我们可以采用巧妙的算法搭配合适的数据结构，如Bloom filter/Hash/bit-map/堆/trie树。

针对空间，无非就一个办法：大而化小，分而治之（hash映射）。

0.1 算法/数据结构基础

0.1.1 Bitmap

所谓的Bit-map就是用一个bit位来标记某个元素对应的值。由于采用了Bit为单位来存储数据，因此在存储空间方面，可以大大节省。例如：我们要对0-7内的5个元素(4,7,2,5,3)排序（这里假设这些元素没有重复）;那么我们就可以采用Bit-map的方法来达到排序的目的。要表示8个数，我们就只需要8个Bit（1Bytes）;将对应的第四位置为1，最终处理结果如下：

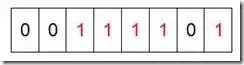
我们只想知道某个元素出现过没有。如果为每个所有可能的值分配1个bit；

但对于海量的、取值分布很均匀的集合进行去重，Bitmap极大地压缩了所需要的内存空间。于此同时，还额外地完成了对原始数组的排序工作。缺点是，Bitmap对于每个元素只能记录1bit信息，如果还想完成额外的功能，恐怕只能靠牺牲更多的空间、时间来完成了。

0.1.2 Bloom Filter(布隆过滤器)

如果说Bitmap对于每一个可能的整型值，通过直接寻址的方式进行映射，相当于使用了一个哈希函数，那布隆过滤器就是引入了k(k>1)个相互独立的哈希函数，保证在给定的空间、误判率下，完成元素判重的过程。下图中是k=3时的布隆过滤器。

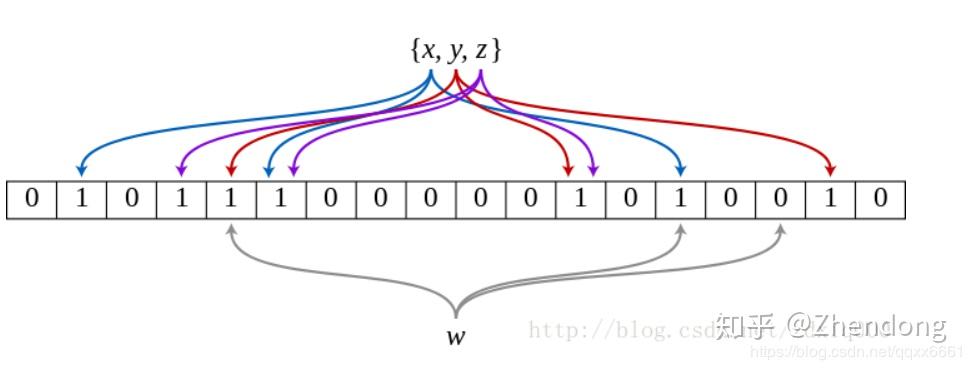
那么布隆过滤器的误差有多少？我们假设所有哈希函数散列足够均匀，散列后落到Bitmap每个位置的概率均等。

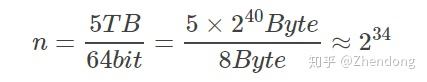
若以m=16nm=16n计算，Bitmap集合的大小为238bit=235Byte=32GB238bit=235Byte=32GB，此时的ε≈0.0005。并且要知道，以上计算的都是误差的上限。

布隆过滤器通过引入一定错误率，使得海量数据判重在可以接受的内存代价中得以实现。从上面的公式可以看出，随着集合中的元素不断输入过滤器中(nn增大)，误差将越来越大。但是，当Bitmap的大小mm（指bit数）足够大时，比如比所有可能出现的不重复元素个数还要大10倍以上时，错误概率是可以接受的。

这里有一个google实现的布隆过滤器，我们来看看它的误判率：

在这个实现中，Bitmap的集合m、输入的原始数集合n、哈希函数k的取值都是按照上面最优的方案选取的，默认情况下保证误判率ε=0.5k<0.03≈0.55，因而此时k=5。

而还有一个很有趣的地方是，实际使用的却并不是5个哈希函数。实际进行映射时，而是分别使用了一个64bit哈希函数的高、低32bit进行循环移位。注释中包含着这个算法的论文“Less Hashing, Same Performance: Building a Better Bloom Filter”，论文中指明其对过滤器性能没有明显影响。很明显这个实现对于m>232时的支持并不好，因为当大于231−1的下标在算法中并不能被映射到。

0.1.3 堆

堆是一种特殊的二叉树，具备以下两种性质 1）每个节点的值都大于（或者都小于，称为最小堆）其子节点的值 2）树是完全平衡的，并且最后一层的树叶都在最左边这样就定义了一个最大堆。如下图用一个数组来表示堆：

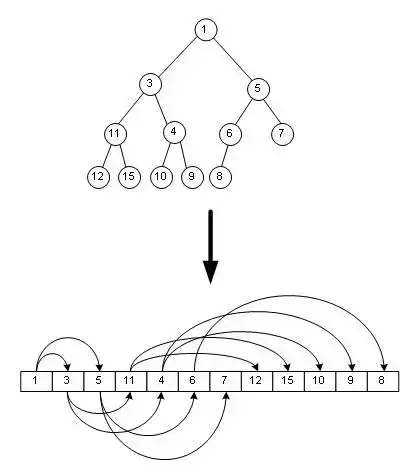
0.1.4 trie树

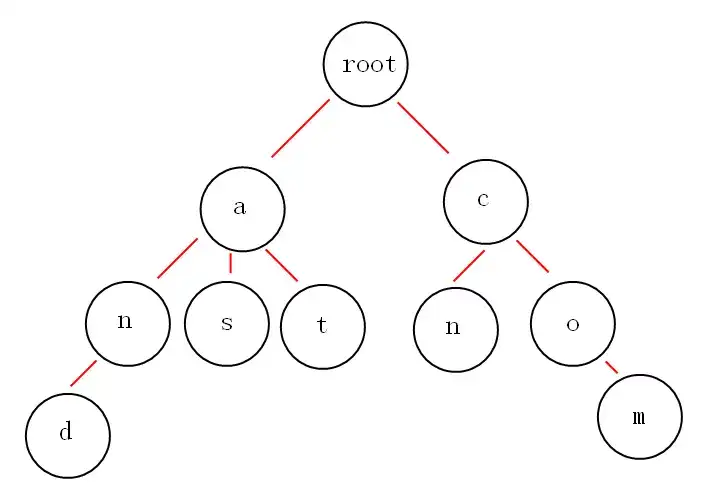
从上面的图中，我们或多或少的可以发现一些好玩的特性。

第一：根节点不包含字符，除根节点外的每一个子节点都包含一个字符。

第二：从根节点到某一节点，路径上经过的字符连接起来，就是该节点对应的字符串。

第三：每个单词的公共前缀作为一个字符节点保存。

适用范围：

前缀统计，词频统计。

0.1.5 外排序

适用范围：

大数据的排序，去重

** 基本原理及要点：**

外部排序的两个独立阶段：

1）首先按内存大小，将外存上含n个记录的文件分成若干长度L的子文件或段。依次读入内存并利用有效的内部排序对他们进行排序，并将排序后得到的有序字文件重新写入外存，通常称这些子文件为归并段。

2）对这些归并段进行逐趟归并，使归并段逐渐由小到大，直至得到整个有序文件为之。

外排序的优化方法：置换选择败者树原理，最优归并树。

2 面试问题解决

2.1 海量日志数据，提取出某日访问百度次数最多的那个IP

算法思想：分而治之+Hash

IP地址最多有2^32=4G种取值情况，所以不能完全加载到内存中处理；
可以考虑采用“分而治之”的思想，按照IP地址的Hash(IP)%1024值，把海量IP日志分别存储到1024个小文件中。这样，每个小文件最多包含4MB个IP地址；
对于每一个小文件，可以构建一个IP为key，出现次数为value的Hash map，同时记录当前出现次数最多的那个IP地址；
可以得到1024个小文件中的出现次数最多的IP，再依据常规的排序算法得到总体上出现次数最多的IP；

2.2 搜索引擎会通过日志文件把用户每次检索使用的所有检索串都记录下来，每个查询串的长度为1-255字节。假设目前有一千万个记录（这些查询串的重复度比较高，虽然总数是1千万，但如果除去重复后，不超过3百万个。一个查询串的重复度越高，说明查询它的用户越多，也就是越热门。），请你统计最热门的10个查询串，要求使用的内存不能超过1G。

可以在内存中处理，典型的Top K算法

算法思想：hashmap+堆

先对这批海量数据预处理，在O（N）的时间内用Hash表完成统计；
借助堆这个数据结构，找出Top K，时间复杂度为O(N*logK)。

或者：采用trie树，关键字域存该查询串出现的次数，没有出现为0。最后用10个元素的最小堆来对出现频率进行排序。

2.3 有一个1G大小的一个文件，里面每一行是一个词，词的大小不超过16字节，内存限制大小是1M。返回频数最高的100个词。

算法思想：分而治之 + hash统计 + 堆排序

顺序读文件中，对于每个词x，取hash(x)%5000，然后按照该值存到5000个小文件（记为x0,x1,…x4999）中。这样每个文件大概是200k左右。如果其中的有的文件超过了1M大小，还可以按照类似的方法继续往下分，直到分解得到的小文件的大小都不超过1M。
对每个小文件，采用trie树/hash_map等统计每个文件中出现的词以及相应的频率。
取出出现频率最大的100个词（可以用含100个结点的最小堆）后，再把100个词及相应的频率存入文件，这样又得到了5000个文件。最后就是把这5000个文件进行归并（类似于归并排序）的过程了。

2.4 有10个文件，每个文件1G，每个文件的每一行存放的都是用户的query，每个文件的query都可能重复。要求你按照query的频度排序。

方案1：

算法思想：分而治之 + hash统计 + 堆排序

顺序读取10个文件，按照hash(query)%10的结果将query写入到另外10个文件中。这样新生成的文件每个的大小大约也1G，大于1G继续按照上述思路分。
找一台内存在2G左右的机器，依次对用hash_map(query, query_count)来统计每个query出现的次数。利用快速/堆/归并排序按照出现次数进行排序。将排序好的query和对应的query_cout输出到文件中。这样得到了10个排好序的文件（记为）。
对这10个文件进行归并排序（内排序与外排序相结合）。

方案2：

算法思想：hashmap+堆

一般query的总量是有限的，只是重复的次数比较多而已，可能对于所有的query，一次性就可以加入到内存了。这样，我们就可以采用trie树/hash_map等直接来统计每个query出现的次数，然后按出现次数做快速/堆/归并排序就可以了。

2.5 给定a、b两个文件，各存放50亿个url，每个url各占64字节，内存限制是4G，让你找出a、b文件共同的url

方案1：可以估计每个文件安的大小为5G×64=320G，远远大于内存限制的4G。所以不可能将其完全加载到内存中处理。考虑采取分而治之的方法。

**算法思想：分而治之 + hash统计 **

遍历文件a，对每个url求取hash(url)%1000，然后根据所取得的值将url分别存储到1000个小文件（记为a0,a1,…,a999）中。这样每个小文件的大约为300M。
遍历文件b，采取和a相同的方式将url分别存储到1000小文件（记为b0,b1,…,b999）。这样处理后，所有可能相同的url都在对应的小文件（a0vsb0,a1vsb1,…,a999vsb999）中，不对应的小文件不可能有相同的url。然后我们只要求出1000对小文件中相同的url即可。
求每对小文件中相同的url时，可以把其中一个小文件的url存储到hash_set中。然后遍历另一个小文件的每个url，看其是否在刚才构建的hash_set中，如果是，那么就是共同的url，存到文件里面就可以了。

方案2：如果允许有一定的错误率，可以使用Bloom filter，4G内存大概可以表示340亿bit。将其中一个文件中的url使用Bloom filter映射为这340亿bit，然后挨个读取另外一个文件的url，检查是否与Bloom filter，如果是，那么该url应该是共同的url（注意会有一定的错误率）。

2.6 在2.5亿个整数中找出不重复的整数，注，内存不足以容纳这2.5亿个整数。

采用2-Bitmap（每个数分配2bit，00表示不存在，01表示出现一次，10表示多次，11无意义）进行，共需内存2^32 * 2 bit=1 GB内存，还可以接受。然后扫描这2.5亿个整数，查看Bitmap中相对应位，如果是00变01，01变10，10保持不变。所描完事后，查看bitmap，把对应位是01的整数输出即可。

2.7 给40亿个不重复的unsigned int的整数，没排过序的，然后再给一个数，如何快速判断这个数是否在那40亿个数当中？

方案1：申请512M的内存，一个bit位代表一个unsigned int值。读入40亿个数，设置相应的bit位，读入要查询的数，查看相应bit位是否为1，为1表示存在，为0表示不存在。

方案2：因为2^32为40亿多，所以给定一个数可能在，也可能不在其中；这里我们把40亿个数中的每一个用32位的二进制来表示假设这40亿个数开始放在一个文件中。

然后将这40亿个数分成两类: 1.最高位为0 2.最高位为1 并将这两类分别写入到两个文件中，其中一个文件中数的个数<=20亿，而另一个>=20亿（这相当于折半了）；与要查找的数的最高位比较并接着进入相应的文件再查找

再然后把这个文件为又分成两类: 1.次最高位为0 2.次最高位为1

并将这两类分别写入到两个文件中，其中一个文件中数的个数<=10亿，而另一个>=10亿（这相当于折半了）；与要查找的数的次最高位比较并接着进入相应的文件再查找。 ……. 以此类推，就可以找到了。

3. 解决问题的一般步骤

3.1 海量数据计算

3.1.1 计算容量

在解决问题之前，要先计算一下海量数据需要占多大的容量。常见的单位换算如下：

1 byte = 8 bit
1 KB = 210 byte = 1024 byte ≈ 103 byte
1 MB = 220 byte ≈ 10 6 byte
1 GB = 230 byte ≈ 10 9 byte
1 亿 = 108

1 个整数占 4 byte，1 亿个整数占 4*108 byte ≈ 400 MB。

3.1.2 拆分

可以将海量数据拆分到多台机器上和拆分到多个文件上：

如果数据量很大，无法放在一台机器上，就将数据拆分到多台机器上。这种方式可以让多台机器一起合作，从而使得问题的求解更加快速。但是也会导致系统更加复杂，而且需要考虑系统故障等问题；
如果在程序运行时无法直接加载一个大文件到内存中，就将大文件拆分成小文件，分别对每个小文件进行求解。

有以下策略进行拆分：

按出现的顺序拆分：当有新数据到达时，先放进当前机器，填满之后再将数据放到新增的机器上。这种方法的优点是充分利用系统的资源，因为每台机器都会尽可能被填满。缺点是需要一个查找表来保存数据到机器的映射，查找表可能会非常复杂并且非常大。
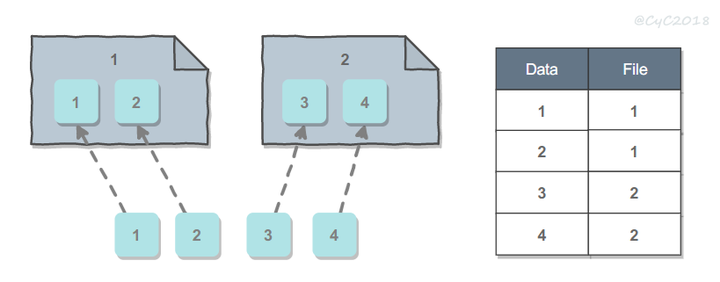
按散列值拆分：选取数据的主键 key，然后通过哈希取模 hash(key)%N 得到该数据应该拆分到的机器编号，其中 N 是机器的数量。优点是不需要使用查找表，缺点是可能会导致一台机器存储的数据过多，甚至超出它的最大容量。
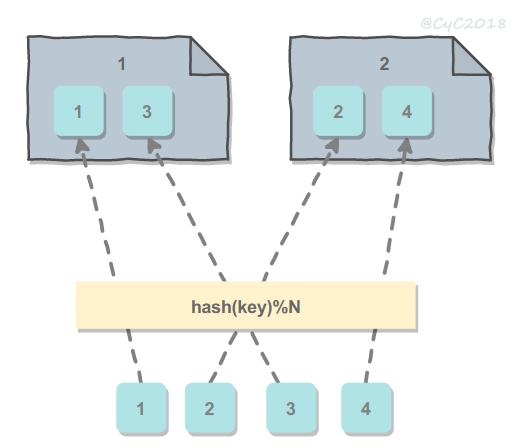
按数据的实际含义拆分：例如一个社交网站系统，来自同一个地区的用户更有可能成为朋友，如果让同一个地区的用户尽可能存储在同一个机器上，那么在查找一个用户的好友信息时，就可以避免到多台机器上查找，从而降低延迟。缺点同样是需要使用查找表。

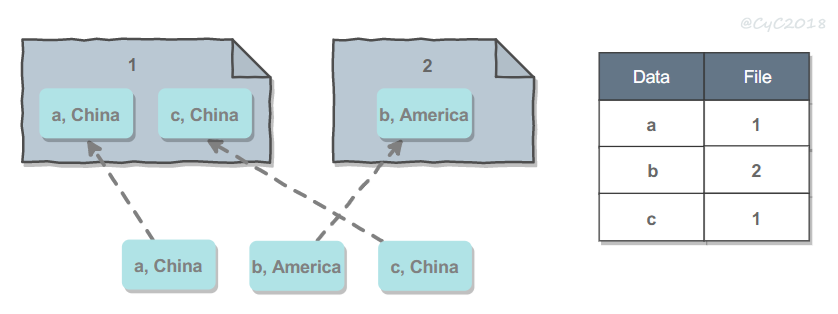
3.1.3 整合

拆分之后的结果还只是局部结果，需要将局部结果汇总为整体的结果。

注：大部分海量数据都可以使用hash取模来处理，因为同一个值hash取模后一定会分配到同一个位置。如果内存实在小，N的值可以取大一些。再者，Hadoop和spark也是处理海量数据的方案，不过非大数据方向应该不做要求。

3.2 海量数据去重问题

3.2.1 问题描述

对于海量数据，要求判断一个数据是否已经存在。这个数据很有可能是字符串，例如 URL。

3.2.2 基本的数据结构

HashSet
- 考虑到数据是海量的，那么就需要使用拆分的方式将数据拆分到多台机器上，分别在每台机器上使用 HashSet 存储。我们需要使得相同的数据拆分到相同的机器上，可以使用哈希取模的拆分方式进行实现。

BitSet

如果海量数据是整数，并且范围不大时，就可以使用 BitSet 存储。通过构建一定大小的比特数组，并且让每个整数都映射到这个比特数组上，就可以很容易地知道某个整数是否已经存在。因为比特数组比整型数组小的多，所以通常情况下单机就能处理海量数据。

class BitSet {
    int[] bitset;
    
    public BitSet(int size) {
        bitset = new int[(size >> 5) + 1]; // divide by 32
    }
    
    boolean get(int pos) {
        int wordNumber = (pos >> 5); // divide by 32
        int bitNumber = (pos & 0x1F); // mod 32
        return (bitset[wordNumber] & (1 << bitNumber)) != 0;
    }
    
    void set(int pos) {
        int wordNumber = (pos >> 5); // divide by 32
        int bitNumber = (pos & 0x1F); // mod 32
        bitset[wordNumber] |= 1 << bitNumber;
    }

布隆过滤器
- 布隆过滤器能够以极小的空间开销解决海量数据判重问题，但是会有一定的误判概率。它主要用在网页黑名单系统、垃圾邮件过滤系统、爬虫的网址判重系统。
- 布隆过滤器也是使用 BitSet 存储数据，但是它进行了一定的改进，从而解除了 BitSet 要求数据的范围不大的限制。在存储时，它要求数据先经过 k 个哈希函得到 k 个位置，并将 BitSet 中对应位置设置为 1。在查找时，也需要先经过 k 个哈希函数得到 k 个位置，如果所有位置上都为 1，那么表示这个数据存在。
- 由于哈希函数的特点，两个不同的数通过哈希函数得到的值可能相同。如果两个数通过 k 个哈希函数得到的值都相同，那么使用布隆过滤器会将这两个数判为相同。
- 可以知道，令 k 和 m 都大一些会使得误判率降低，但是这会带来更高的时间和空间开销。
- 布隆过滤器会误判，也就是将一个不存在的数判断为已经存在，这会造成一定的问题。例如在垃圾邮件过滤系统中，会将一个邮件误判为垃圾邮件，那么就收不到这个邮件。可以使用白名单的方式进行补救。

前缀树(Trie)

class Trie {
    private class Node {
        Node[] childs = new Node[26];
        boolean isLeaf;
    }
    
    private Node root = new Node();
    
    public Trie() {
    }
    
    public void insert(String word) {
        insert(word, root);
    }
    
    private void insert(String word, Node node) {
        if (node == null) return;
        if (word.length() == 0) {
            node.isLeaf = true;
            return;
        }
        int index = indexForChar(word.charAt(0));
        if (node.childs[index] == null) {
            node.childs[index] = new Node();
        }
        insert(word.substring(1), node.childs[index]);
    }
    
    public boolean search(String word) {
        return search(word, root);
    }
    
    private boolean search(String word, Node node) {
        if (node == null) return false;
        if (word.length() == 0) return node.isLeaf;
        int index = indexForChar(word.charAt(0));
        return search(word.substring(1), node.childs[index]);
    }
    
    public boolean startsWith(String prefix) {
        return startWith(prefix, root);
    }
    
    private boolean startWith(String prefix, Node node) {
        if (node == null) return false;
        if (prefix.length() == 0) return true;
        int index = indexForChar(prefix.charAt(0));
        return startWith(prefix.substring(1), node.childs[index]);
    }
    
    private int indexForChar(char c) {
        return c - 'a';
    }
}

1. N个数求前K大

快排pivot
计数排序，开辟一个大数组，记录每个整数出现的次数，从大到小取（bitmap）
维护一个大小为k的大根堆

2. 求文件A中没有但B中有的单词(字典树)

遍历文件A，将文件hash到n个小文件中
对B文件同样操作
然后对于每一对文件，进行hash操作

3. 海量数据排序问题

hash到小文件中，然后在小文件排序。然后合并的时候，用堆，每个小文件取一个，然后最小的拿走再加入对应文件的数字，直到结束。
如果要求文件IO次数尽量少，比如：一个文件中20亿个int，有重复但不超过10000个，排序后输出到另一个文件（要求减少文件IO）

4. 海量数据出现次数最多数据

hash进行文件分发
但是内存有限制的话，可以先分段到小文件中，然后再hash
直接hash到小文件，再在小文件hash，避免集中在一个区间造成退化
如果数据给的是40亿都是一个数字，那这个数字的index计数就会爆掉（int最大21亿左右），可以把初始值设置为-21亿
如果增加到80亿呢？一边遍历一边判断，如果超过40亿，也不可能有比它更多的了，直接返回

5. 40亿整数，再给一个新数字，判断是否在40亿当中

分布式机器，多台机器一起查找并合并
bitmap，注意不是40亿个数字就要40亿个位，而是都是整数，所以覆盖所有整数范围就是2^32大概42亿，所以需要申请2^32个位，一个int8个位，所以需要2^29个int，占用500M内存

6. 10亿个数值，找最大的一万个？

应该计算一下这个数组整体大小，然后询问数据是否重复，如果重复，先对文件hash，然后保存不同文件。维持一个1万的小顶堆，遍历效率是o(nlogn)

面试海量数据问题

2021 暑期实习