3月14号腾讯一面面经
2020-03-14 10:47:53
概要信息记录表
| 项目 | 定义 |
|---|---|
| 通知时间 | 2020-03-13 22:00 |
| 通知方式 | 邮件通知 |
| 面试日期 | 2020-03-14 |
| 面试时间 | 09:57-10:40 |
| 结果 | 通过,等待复试 |
面试问题记录
0. 本科是不是计算机
答:不是研究生考研考的计算机;高中的时候不知道自己要学什么。到大二才发现自己对计算机很感兴趣,所以自学计算机知识并考研 -: 那那些知识点都清楚吗? -: 清楚吧,毕竟考过研
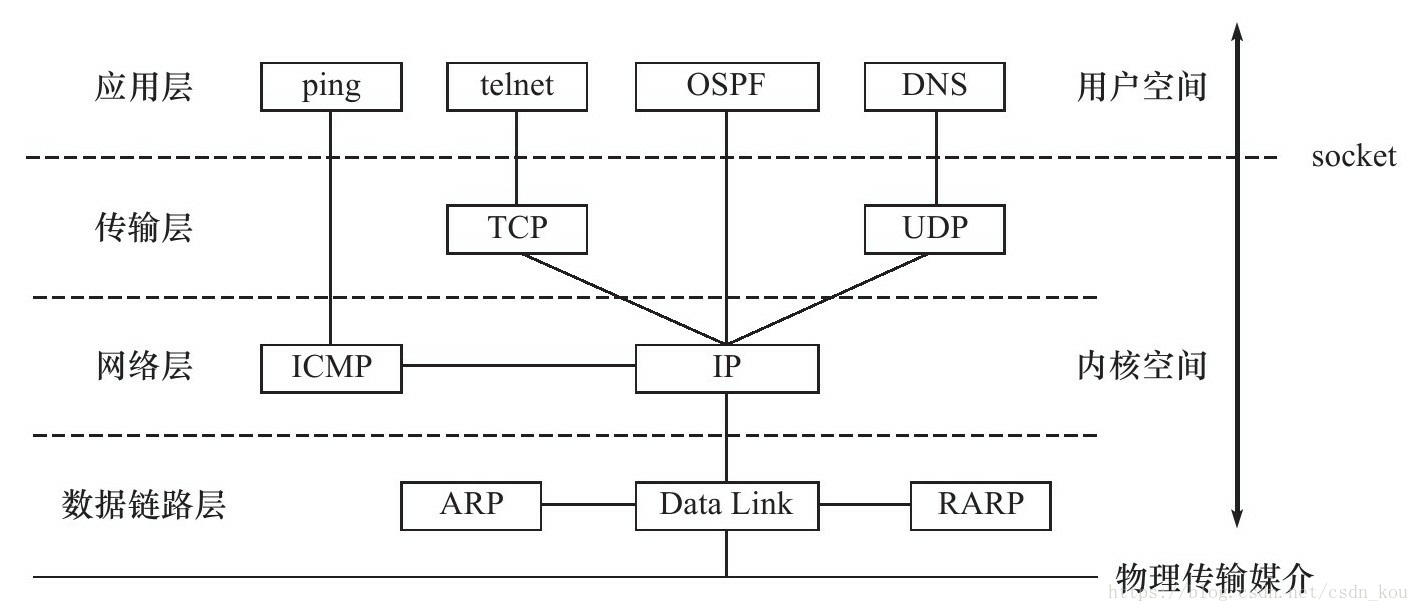
1. 说一下TCP/IP的四层网络模型
答:应用层,有http和DNS等;传输层:TCP/UDP;网络层:IP/ICMP;数据链路层等
标准答案
参考链接:
1. 长连接和短连接;他们各自拥有什么优点和缺点
答:按照自己的意想;说了一通
标准答案
参考链接:
1.1 短连接:
- 连接->传输数据->关闭连接
- 比如HTTP是无状态的的短链接,浏览器和服务器每进行一次HTTP操作,就建立一次连接,但任务结束就中断连接。
- 因为连接后接收了数据就断开了,所以每次数据接受处理不会有联系。 这也是HTTP协议无状态的原因之一。
1.2 长连接:
- 连接->传输数据->保持连接 -> 传输数据-> ………..->直到一方关闭连接,多是客户端关闭连接。
- 长连接指建立SOCKET连接后不管是否使用都保持连接,但安全性较差。
1.3 什么时候用长连接,短连接?
长连接多用于操作频繁,点对点的通讯,而且连接数不能太多情况,。每个TCP连接都需要三步握手, 这需要时间,如果每个操作都是先连接,再操作的话那么处理速度会降低很多,所以每个操作完后都 不断开,次处理时直接发送数据包就OK了,不用建立TCP连接。例如:数据库的连接用长连接, 如果 用短连接频繁的通信会造成socket错误,而且频繁的socket 创建也是对资源的浪费。
而像WEB网站的http服务一般都用短链接,因为长连接对于服务端来说会耗费一定的资源,而像WEB网 站这么频繁的成千上万甚至上亿客户端的连接用短连接会更省一些资源,如果用长连接,而且同时有成 千上万的用户,如果每个用户都占用一个连接的话,那可想而知吧。所以并发量大,但每个用户无需频 繁操作情况下需用短连好。
1.4 发送接收方式
1、异步
报文发送和接收是分开的,相互独立的,互不影响。这种方式又分两种情况: (1)异步双工:接收和发送在同一个程序中,由两个不同的子进程分别负责发送和接收 (2)异步单工:接收和发送是用两个不同的程序来完成。
2、同步
报文发送和接收是同步进行,既报文发送后等待接收返回报文。 同步方式一般需要考虑超时问题,即报文发出去后不能无限等待,需要设定超时时间,超过该时间发送方不再等待读返回报文,直接通知超时返回。 在长连接中一般是没有条件能够判断读写什么时候结束,所以必须要加长度报文头。读函数先是读取报文头的长度,再根据这个长度去读相应长度的报文。
2. 说一下https的大致过程
https主要工作流程如下:
- 客户端将自己支持的一套加密规则发送给服务端
- 服务端从中选出一组加密算法和hash算法,并将自己的身份信息以证书的形式发回给客户端。证书里面包含了服务端的地址,加密公钥,以及证书的颁发机构
- 客户端获得网站的证书后,先验证证书的合法性,如果证书时受信任的,或者用户自己接收了不受信任的证书,客户端会生成一串随机数的密码,并用证书中提供的公钥加密
- 客户端使用约定好的hash算法计算握手信息,并使用生成的随机数对握手信息进行加密,最后将之前生成的所有信息发送给服务端
- 服务端接收到数据后,先用自己家的私钥将信息解密,把随机数密码取出来,用这个随机数密码去解密握手信息,将握手信息进行hash,验证其是否与发过来的hash值一样
- 然后使用密码加密一段握手信息,发送回客户端
- 客户端解密计算握手信息的hash,如果与服务端发过来的hash是一样的,握手过程结束,连接建立,之后的所有通信数据都由之前的随机数密码并使用对称加密算法进行加密,然后传输
3. https主要攻击的阶段是那个?
答:不知道,估计是模拟客户端发送请求;(其实是中间人攻击)
答案
参考链接:
SSL劫持攻击
SSL劫持也就是SSL证书欺骗攻击,攻击者为了获得HTTPS传输的明文数据,需要先将自己接入到浏览器与目标网站之间(中间人),在传输数据的过程中,替换目标网站发给浏览器的证书,之后解密传输中的数据,简单的图示如下:
[浏览器] <======> [目标网站] (正常情况)
[浏览器] <======> 中间人 <======> [目标网站] (中间人攻击)
中间人攻击最好的环境是在局域网中,局域网中所有的计算机需要通过一个固定的出口(网关)来接入互联网,因此攻击者只需要在局域网中实施一次中间人攻击就可以顺利的截获所有计算机与网关之间传输的数据。
SSLStrip攻击
SSLStrip攻击也需要将攻击者设置为中间人,之后将HTTPS访问替换为HTTP返回给浏览器,由于HTTP协议传输的数据是未加密的,从而截获用户访问的数据。举个例子,当我们访问hotmail.com的时候会重定向到一个https://login.live.com的一个HTTPS的地址上,SSLStrip会代替用户与服务器通信,并将这个地址改为http://login.live.com(注意这个地址在http后面没有s)返回给浏览器,此时如果用户继续登录的话,攻击者就会截取到用户的密码。这种攻击非常对普通用户非常具有迷惑性,但是防御却非常的简单:
第三类攻击
CA证书的具体内容看过吗?
答:没有不知道
参考答案
参考链接:
主要内容:
- 版本号
- 序列号
- 签名算法
- 颁发者
- 有效日期
- 主体:证书拥有者的标识信息
- 主体的公钥信息
- 公钥算法
- 主体公钥
- 颁发者唯一号
- 主体唯一号
- 扩展
说一下http常见的系列状态码
答:1xx,2xx,3xx,4xx,5xx …
答案
参考链接:
Linux中进程间通信的方式有哪些?
答:FIFO、管道、信号量、套接字、共享内存(没有说消息队列)
参考答案 进程间通信的方式
3. Get和POST的区别
答:Get不允许携带body主要字段;POST可以
参考答案
参考链接:
get和post的区别主要有以下几方面:
- url可见性:get,参数url可见;post,url参数不可见
- 数据传输上:get,通过拼接url进行传递参数;post,通过body体传输参数
- 缓存性:get请求是可以缓存的;post请求不可以缓存
- 后退页面的反应:get请求页面后退时,不产生影响;post请求页面后退时,会重新提交请求
- 传输数据的大小:get一般传输数据大小不超过2k-4k(根据浏览器不同,限制不一样,但相差不大);post请求传输数据的大小根据php.ini 配置文件设定,也可以无限大。
- 安全性:这个也是最不好分析的,原则上post肯定要比get安全,毕竟传输参数时url不可见,但也挡不住部分人闲的没事在那抓包玩。安全性个人觉得是没多大区别的,防君子不防小人就是这个道理。对传递的参数进行加密,其实都一样。
- GET在浏览器回退时是无害的,而POST会再次提交请求。
- GET产生的URL地址可以被Bookmark,而POST不可以。
- GET请求会被浏览器主动cache,而POST不会,除非手动设置。
- GET请求只能进行url编码,而POST支持多种编码方式。
- GET请求参数会被完整保留在浏览器历史记录里,而POST中的参数不会被保留。
- GET请求在URL中传送的参数是有长度限制的,而POST么有。
- 对参数的数据类型,GET只接受ASCII字符,而POST没有限制。
- GET比POST更不安全,因为参数直接暴露在URL上,所以不能用来传递敏感信息。
- GET参数通过URL传递,POST放在Request body中。
(大多数)浏览器通常都会限制url长度在2K个字节,而(大多数)服务器最多处理64K大小的url
4. 为什么说post比Get更加安全
答:因为允许使用body可以自定义字段和读写方式(其实有问题;还要考虑到浏览器的记录);
参考答案
参考链接:
主要核心:get 请求的url是在服务器上有日志记录,在浏览器也能查到历史记录,但是post请求的参数都在body里面,服务器日志记录不到,浏览器历史也记录不到
- get是把参数数据队列加到提交表单的action属性所指的url中,值和表单中的各个字段一一对应,在URL中可以看到。post则是通过HTTPpost机制,将表单内各个字段与其内容放置在HTML header 内一起传送到ACTION属性所指的URL地址,用户看不到这个地址
- 对于get方式,服务器端用Request.QueryString获取变量的值,对于post方式,服务器端用Request.Form获取提交的数据;两种方式的参数都可以用Request来获得。
- get传送的数据量较小,不能大于2KB。post传送的数据量较大,一般被默认为不受限制。
- 在不显示后端的ajax来讲,post和get的安全性是一样的
5. 数据库用过吗?
答:上过老师的课,没怎么用过
6. 数据库的索引结构
答:B+树,并且叶子节点相互链接;方便进行范围查找
参考链接
Mysql索引主要有两种结构:B+Tree索引和Hash索引
7. 什么情况下需要建立索引
答:经常查找和检索的时候
参考 索引相关
8. 一个订单表,订单,时间,状态是否适合建立索引
答:索引建立使用B+树,索引关键字应当尽量避免重复。时间是可以的。但是状态属于枚举类型。不适合作为索引
9. 联合索引
答:(听成聚簇索引去了);答了聚簇索引的东西。联合索引key是两个值的联合值,遵循最左原则,左边相同是关键字相同。不同时,再分关键字。
参考答案
参考链接:
联合索引又叫复合索引。对于复合索引:Mysql从左到右的使用索引中的字段,一个查询可以只使用索引中的一部份,但只能是最左侧部分。例如索引是key index (a,b,c)。 可以支持a | a,b| a,b,c 3种组合进行查找,但不支持 b,c进行查找 .当最左侧字段是常量引用时,索引就十分有效。 两个或更多个列上的索引被称作复合索引。
所以说创建复合索引时,应该仔细考虑列的顺序。对索引中的所有列执行搜索或仅对前几列执行搜索时,复合索引非常有用;仅对后面的任意列执行搜索时,复合索引则没有用处。
10 SQL注入
答:不知道
参考链接:
注入的本质,是把用户输入数据作为代码执行。有两个关键条件:第一个是用户能控制输入;第二是原本程序要执行的代码,拼接了用户输入的数据,把数据当代码执行了。
SQL注入原因:
- ①不当的类型处理;
- ②不安全的数据库配置;
- ③不合理的查询集处理;
- ④不当的错误处理;
- ⑤转义字符处理不合适;
- ⑥多个提交处理不当。
解决办法:
- (简单又有效的方法)PreparedStatement
采用预编译语句集,它内置了处理SQL注入的能力,只要使用它的setXXX方法传值即可。
使用好处:
(1).代码的可读性和可维护性.
(2).PreparedStatement尽最大可能提高性能.
(3).最重要的一点是极大地提高了安全性.
原理:
sql注入只对sql语句的准备(编译)过程有破坏作用 而PreparedStatement已经准备好了,执行阶段只是把输入串作为数据处理,而不再对sql语句进行解析,准备,因此也就避免了sql注入问题.
- 使用正则表达式过滤传入的参数
要引入的包:
import java.util.regex.*;
//正则表达式:
private String CHECKSQL = “^(.+)\sand\s(.+)|(.+)\sor(.+)\s$”;
//判断是否匹配:
Pattern.matches(CHECKSQL,targerStr);
//下面是具体的正则表达式:
//检测SQL meta-characters的正则表达式 :
/(\%27)|(\’)|(\-\-)|(\%23)|(#)/ix
//修正检测SQL meta-characters的正则表达式 :
/((\%3D)|(=))[^\n]*((\%27)|(\’)|(\-\-)|(\%3B)|(:))/i
//典型的SQL 注入攻击的正则表达式 :
/\w*((\%27)|(\’))((\%6F)|o|(\%4F))((\%72)|r|(\%52))/ix
//检测SQL注入,UNION查询关键字的正则表达式 :
/((\%27)|(\’))union/ix(\%27)|(\’)
//检测MS SQL Server SQL注入攻击的正则表达式:
/exec(\s|)+(s|x)p\w+/ix
//等等
- 字符串过滤
比较通用的一个方法:
| ( |
public static boolean sql_inj(String str)
{
String inj_str = "'|and|exec|insert|select|delete|update|
count|*|%|chr|mid|master|truncate|char|declare|;|or|-|+|,";
String inj_stra[] = split(inj_str,"|");
for(int i=0 ; i < inj_stra.length ; i++ )
{
if (str.indexOf(inj_stra[i])>=0)
{
return true;
}
}
return false;
}
- jsp中调用该函数检查是否包函非法字符防止SQL从URL注入;sql_inj.java代码:
package sql_inj;
import java.net.*;
import java.io.*;
import java.sql.*;
import java.text.*;
import java.lang.String;
public class sql_inj{
public static boolean sql_inj(String str)
{
String inj_str = "'|and|exec|insert|select|delete|update|
count|*|%|chr|mid|master|truncate|char|declare|;|or|-|+|,";
//这里的东西还可以自己添加
String[] inj_stra=inj_str.split("\|");
for (int i=0 ; i < inj_stra.length ; i++ )
{
if (str.indexOf(inj_stra[i])>=0)
{
return true;
}
}
return false;
}
}
- JSP页面判断代码: 使用javascript在客户端进行不安全字符屏蔽
功能介绍:检查是否含有”‘”,”\”,”/”
参数说明:要检查的字符串
返回值:0:是1:不是
函数名是
function check(a)
{
return 1;
fibdn = new Array (”‘” ,”\”,”/”);
i=fibdn.length;
j=a.length;
for (ii=0; ii<i; ii++)
{ for (jj=0; jj<j; jj++)
{ temp1=a.charAt(jj);
temp2=fibdn[ii];
if (tem’; p1==temp2)
{ return 0; }
}
}
return 1;
}
11 算法题:
11.1 两数之和
11.2 能否将时间复杂度更改为O(n)
参考链接:
4月9日腾讯IEG面经
2020-04-09 15:30:56
2.1 说一下你的项目
2.1 项目中使用了多线程;它们之间的通信方式有哪些?(只说了自己项目中用到了锁,因该说全的)
- 临界区:使用内存屏障和锁创建临界区
- 互斥量:锁;``
- 信号量;
sem_wait(sem_t *sem)/sem_post(sem_t *sem) - 条件变量:
pthread_cond_init;pthread_cond_signal;pthread_cond_wait
2.2 进程间的通信方式
- 管道
- 命名管道
- 消息队列
- 信号/信号量
- 共享内存
- 套接字
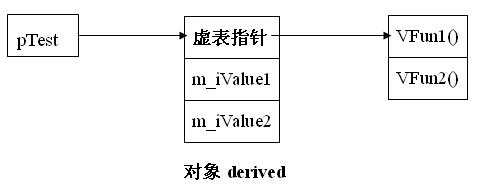
2.3 C++ 类里面的内存结构;虚指针位置在变量开始吗?
- 浅析C++中虚函数的调用及对象的内部布局
- 浅析C++中的this指针
- c++中除了虚指针和成员变量,函数并不在类的内存中。并且虚指针在头部。也就是成员变量之上。
2.4 malloc的系统调用(没有答出来)
应该是小于128KB使用brk,大于128KB使用mmap直接映射。(详见百度面试准备1.37)
2.5 Linux的虚拟内存
- 原因
- 特点
- 代价
- Linux中的段页式的管理方式
- 虚拟内存置换的方式
2.6 TCP和UDP首部的大小和关键字段
TCP大小是20字节,UDP大小是8字节;详细内容见:5.51 TCP和UDP,IP的大小以及关键字段结构。
2.7 玩过游戏吗?
玩过QQ飞车
2.8 QQ飞车移动之间传输数据应该怎么传输
只传输关键节点,比如相对的x,y,z坐标。
2.9 传输应该使用TCP还是UDP;为什么,该怎么设计?
对于实时性要求比较高;应该使用UDP,说了一下TCP和UDP的区别,为了保证传输的稳定性UDP应该如何改进,但是为了保证其有序性,应该使用序号和确认号。对于确认重传和滑动窗口可以使用多次发送相同帧,用带宽换准确度。唯一比较麻烦的是拥塞控制,无法解决和避免。 (详见5.50 TCP,UDP应用场景,即要求速度,又要求可靠性怎么办)
3.0 编程题三道(两个小时,只写了两道)
3.0.1 链表中环的入口节点(总是有测试用例过不了)
/*
struct ListNode {
int val;
struct ListNode *next;
ListNode(int x) :
val(x), next(NULL) {
}
};
*/
/*
使用快慢指针查看是否存在重合节点
然后再找到
*/
class Solution {
public:
ListNode* EntryNodeOfLoop(ListNode* pHead)
{
//注意这里进行检查
if(!pHead||!pHead->next) return nullptr;
ListNode *slow=pHead;
ListNode *fast=pHead;
while(fast&&fast->next){
fast=fast->next->next;
slow=slow->next;
if(slow==fast){
break;
}
}
if(slow!=fast){
return nullptr;
}
slow=pHead;
while(slow&&fast){
if(slow==fast){
break;
}
slow=slow->next;
fast=fast->next;
}
return slow;
}
};
3.0.2 surrounded-regions
/*
主要思路:从边界开始对边界的所有值进行BFS
将BFS到的节点都转变为M;
然后将非M的O全部设置为X;
将M设置为O;
*/
class Solution {
public:
void solve(vector<vector<char>> &board) {
if(board.empty()) return ;
for(int i=0;i<board.size();++i){
if(board[i][0]=='O'){
BFS(board,i,0);
}
}
for(int i=0;i<board[0].size();++i){
if(board[0][i]=='O'){
BFS(board,0,i);
}
}
if(board.size()>1){
int len=board.size()-1;
for(int i=0;i<board[0].size();++i){
if(board[len][i]=='O'){
BFS(board,len,i);
}
}
}
if(board[0].size()>1){
int len=board[0].size()-1;
for(int i=0;i<board.size();++i){
if(board[i][len]=='O'){
BFS(board,i,len);
}
}
}
for(int i=0;i<board.size();++i){
for(int j=0;j<board[0].size();++j){
if(board[i][j]=='O'){
board[i][j]='X';
}
}
}
for(int i=0;i<board.size();++i){
for(int j=0;j<board[0].size();++j){
if(board[i][j]=='M'){
board[i][j]='O';
}
}
}
};
int dxdy[4][2]={
{-1,0},
{0,-1},
{1,0},
{0,1}
};
void BFS(vector<vector<char>> &board,int x,int y){
if(x<0||x>=board.size()||y<0||y>=board[0].size()){
return ;
}
if(board[x][y]!='O') return ;
board[x][y]='M';
for(int i=0;i<4;++i){
int dx=dxdy[i][0];
int dy=dxdy[i][1];
BFS(board,x+dx,y+dy);
}
}
};
3.0.3 派对的最大快乐值
/*
主要思路:使用深度遍历;对每个节点
存储其child 子集和对应的happy值
并进行DFS更新
分为当前去还是不去,去则将查找找孙节点的所有去的子集并添加
不去,则直接计算所有子节点的子集
比较去和不去的最大值
*/
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
struct Node{
int happy_val=0;
int max_happy=0;
vector<int> childs;
friend ostream& operator << (ostream &os,const Node & no){
os<<"happy:"<<no.happy_val<<"max_happy "<<no.max_happy<<"\t";
os<<"childs: ";
for(int i=0;i<no.childs.size();++i){
cout<<"child "<<"i: "<<no.childs.at(i)<<" ";
}
os<<endl;
return os;
}
};
//深度遍历返回其最大值
int DFS(vector<Node>& tree,int index)
{
if(index>=tree.size()||index<=0) return 0;
auto& temp_node=tree.at(index);
//页节点直接返回当前值
if(temp_node.childs.empty()){
return temp_node.happy_val;
}
if(temp_node.max_happy!=0){
return temp_node.max_happy;
}
int sum1=0,sum2=temp_node.happy_val;
//使用当前节点
for(int i=0;i<temp_node.childs.size();++i){
//不使用当前节点
sum1+=DFS(tree,temp_node.childs.at(i));
//使用当前节点;计算孙节点
int child_node=temp_node.childs.at(i);
for(int j=0;j<tree.at(child_node).childs.size();++j){
sum2+=DFS(tree,tree.at(child_node).childs.at(j));
}
}
temp_node.max_happy=max(sum1,sum2);
return temp_node.max_happy;
}
int main(int argc ,char* argv[]){
int n=0;
int root=1;
cin>>n>>root;
vector<Node> tree(n+1);
int i=0;
while(i<n)
{
cin>>tree.at(i+1).happy_val;
++i;
}
i=0;
while(i<n){
int parent=0,son=0;
cin>>parent>>son;
tree.at(parent).childs.emplace_back(son);
++i;
}
cout<<DFS(tree,root)<<endl;
return 0;
}
阿里菜鸟一面
2020-04-10 15:30
1. 算法题,马走棋盘
/*
主要思路:使用数组作为数据存储结构,
第一个到达的肯定是步数最少的。
*/
#include <iostream>
#include <queue>
#include <stack>
using namespace std;
#define N 8
struct Position
{
int x;
int y;
};
int PositionToIndex(const Position& pos)
{
return pos.x * N + pos.y;
}
Position IndexToPosition(int index)
{
Position pos = { index / N, index % N };
return pos;
}
bool IsValid(const Position& pos)
{
return (pos.x >= 0 && pos.x < N && pos.y >= 0 && pos.y < N);
}
int main(int argc, char* argv[])
{
// 将棋盘延展成一维数组,序号表示当前格子,对应的值表示上一步的格子序号
int* array = new int[N*N];
for (int i = 0; i < N*N; i++)
{
array[i] = -1;
}
// 指定起始和结束位置
Position start, end;
start.x = 3;
start.y = 4;
end.x = N - 1;
end.y = N - 1;
bool finished = false;
// 用栈存储每一步的序列位置,之后可反转输出
stack<int> finishSteps;
// 利用队列实现广度优先搜索
queue<Position> steps;
steps.push(start);
// 由于是第一步,约定值为-2,表示没有上一步
array[PositionToIndex(start)] = -2;
// 队列里的数据存储当前能走到的格子,若已为空表示已走完所有的格式,或所能走完的格子
while (!steps.empty())
{
// 取出当前的格子,计算下一步,并将当前格子移出队列
Position curPos = steps.front();
int curIndex = PositionToIndex(curPos);
steps.pop();
// 已走到指定终点
if (curPos.x == end.x && curPos.y == end.y)
{
finishSteps.push(PositionToIndex(end)); // 当前一步入栈
int lastStep = curIndex;
while (true)
{
// 一直找上一步,找到起始点为止
lastStep = array[lastStep];
if (lastStep == -2)
{
finished = true;
break;
}
else
{
finishSteps.push(lastStep);
}
}
break;
}
// 下一步有8个可走的情况,超出边界,或已探索到的忽略
Position pos1 = { curPos.x + 1, curPos.y - 2 };
if (IsValid(pos1))
{
int index1 = PositionToIndex(pos1);
if (array[index1] == -1)
{
steps.push(pos1);
array[index1] = curIndex;
}
}
Position pos2 = { curPos.x + 2, curPos.y - 1 };
if (IsValid(pos2))
{
int index2 = PositionToIndex(pos2);
if (array[index2] == -1)
{
steps.push(pos2);
array[index2] = curIndex;
}
}
Position pos3 = { curPos.x + 2, curPos.y + 1 };
if (IsValid(pos3))
{
int index3 = PositionToIndex(pos3);
if (array[index3] == -1)
{
steps.push(pos3);
array[index3] = curIndex;
}
}
Position pos4 = { curPos.x + 1, curPos.y - 2 };
if (IsValid(pos4))
{
int index4 = PositionToIndex(pos4);
if (array[index4] == -1)
{
steps.push(pos4);
array[index4] = curIndex;
}
}
Position pos5 = { curPos.x - 1, curPos.y + 2 };
if (IsValid(pos5))
{
int index5 = PositionToIndex(pos5);
if (array[index5] == -1)
{
steps.push(pos5);
array[index5] = curIndex;
}
}
Position pos6 = { curPos.x - 2, curPos.y + 1 };
if (IsValid(pos6))
{
int index6 = PositionToIndex(pos6);
if (array[index6] == -1)
{
steps.push(pos6);
array[index6] = curIndex;
}
}
Position pos7 = { curPos.x - 2, curPos.y - 1 };
if (IsValid(pos7))
{
int index7 = PositionToIndex(pos7);
if (array[index7] == -1)
{
steps.push(pos7);
array[index7] = curIndex;
}
}
Position pos8 = { curPos.x - 1, curPos.y - 2 };
if (IsValid(pos8))
{
int index8 = PositionToIndex(pos8);
if (array[index8] == -1)
{
steps.push(pos8);
array[index8] = curIndex;
}
}
}
// 完成,打印
if (finished)
{
while (!finishSteps.empty())
{
Position pos = IndexToPosition(finishSteps.top());
cout << "(" << pos.x << ", " << pos.y << "), ";
finishSteps.pop();
}
cout << endl;
}
delete[] array;
system("pause");
return 0;
}